Winograd算法

Winograd算法是Shmuel Winograd在1980年提出的用来减少FIR滤波器计算量的一个算法（这里的grad和梯度没有关系），但当时并没有引起太多关注。直到后来人们发现此算法可以用来加速CNN网络的卷积运算，才得到广泛应用。

Winograd

考虑一个一维卷积，输入信号 $d = [d_{0}, d_{1}, d_{2}, d_{3}]^{T}$ ，卷积核 $g = [g_{0}, g_{1}, g_{2}]^{T}$ ，输出为 $r = [r_{0}, r_{1}]^{T}$ ，则有：

F = [d_{0} d_{1} d_{1} d_{2} d_{2} d_{3}] g_{0} g_{1} g_{2} = [d_{0} g_{0} + d_{1} g_{1} + d_{2} g_{2} d_{1} g_{0} + d_{2} g_{1} + d_{3} g_{2}] = [r_{0} r_{1}]

但是可以观察到，计算中存在重复，例如 $d_{1}$ 和 $d_{2}$ 。这些计算一共用到了6次乘法和4次加法。现在做如下变换，记

m_{1} = (d_{0} - d_{2}) g_{0} m_{2} = (d_{1} + d_{2}) \frac{g _{0} + g _{1} + g _{2}}{2}

m_{4} = (d_{1} - d_{3}) g_{2} m_{3} = (d_{2} - d_{1}) \frac{g _{0} - g _{1} + g _{2}}{2}

则有：

F = [r_{0} r_{1}] = [m_{1} + m_{2} + m_{3} m_{2} - m_{3} - m_{4}]

因为卷积核事先已知，含 $g$ 的式子可以提前算好，因此只需计算 $m_{1}$ ~ $m_{4}$ （各1次乘法、1次加法）和 $r_{0}$ 、 $r_{1}$ （各2次加法），总共4次乘法和8次加法。

乘法通常比加法耗时更长，因此减少乘法次数可以提高计算效率。

Winograd已经证明了对于卷积核长度为 $r$ 的一维卷积，计算 $m$ 个输出所需的最少乘法数量为 $m + r - 1$ 。将上面的计算过程写成矩阵形式为：

F = A^{T} [(G g) ⊙ (B^{T} d)]

其中的 $⊙$ 是哈达玛积(Hadamard Product)，代表逐元素乘积。

$G$ 是卷积核变换矩阵，尺寸为 $(m + r - 1) \times r$ ，对应到上例有：

G g = 1 \frac{1}{2} \frac{1}{2} 0 0 \frac{1}{2} - \frac{1}{2} 0 0 \frac{1}{2} \frac{1}{2} 1 g_{0} g_{1} g_{2} = g_{0} \frac{g _{0} + g _{1} + g _{2}}{2} \frac{g _{0} - g _{1} + g _{2}}{2} g_{2}

$B^{T}$ 是输入变换矩阵，尺寸为 $(m + r - 1) \times (m + r - 1)$ ，对应到上例有：

B^{T} d = 1000 01 - 1 1 - 1 110 000 - 1 d_{0} d_{1} d_{2} d_{3} = d_{0} - d_{2} d_{1} + d_{2} d_{2} - d_{1} d_{1} - d_{3}

$A^{T}$ 是输出变换矩阵，尺寸为 $m \times (m + r - 1)$ ，对应到上例有：

A^{T} = [1011 1 - 1 0 - 1]

推广到二维情形，假设输入是 $4 \times 4$ 图像，卷积核大小 $3 \times 3$ ，则首先通过Img2col展开成矩阵乘法，再分块使用Winograd。

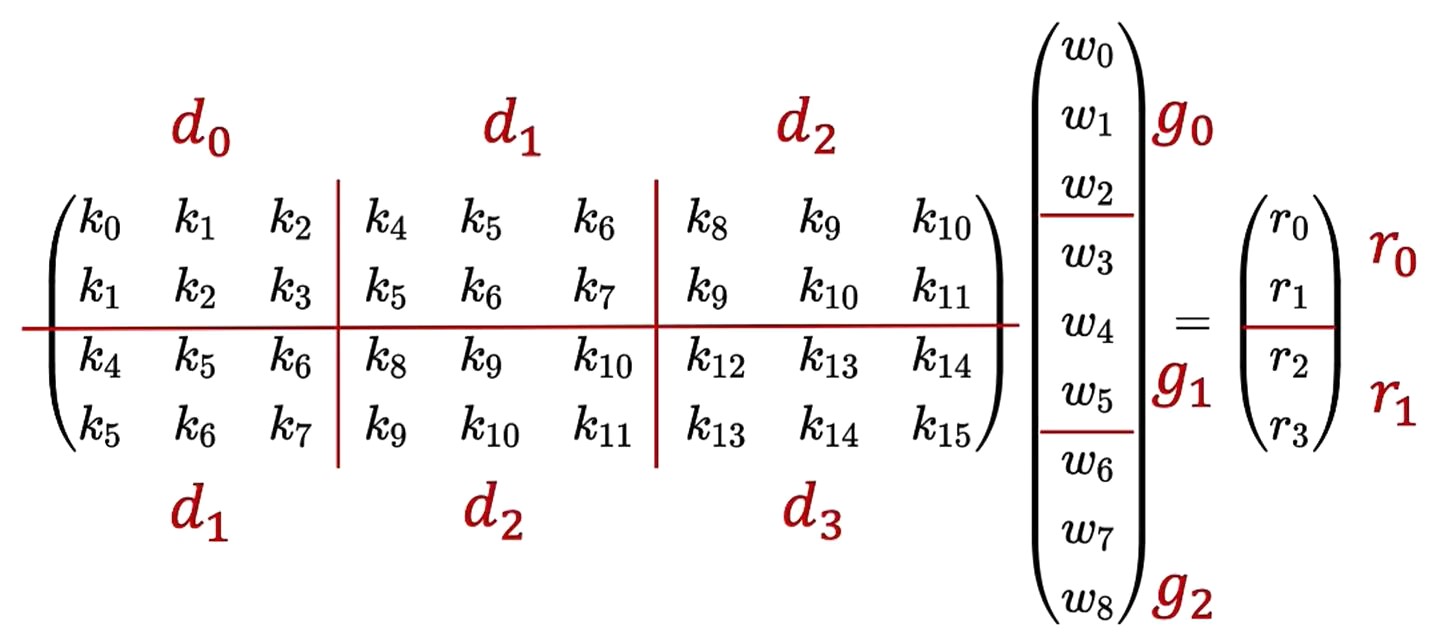
对于划分的每一小块，都可以使用一维Winograd算法计算；而整体来看，如果把每个分块都当作一个元素，则同理可以再用一次一维Winograd算法计算。

从计算的效率来说，先分析整体，对分块矩阵进行Winograd算法，这时会需要4次矩阵乘；而每次矩阵乘再用Winograd算法，需要4次数乘，整个过程共需要16次乘法。如果使用常规的卷积操作则需要36次乘法。

Winograd算法通过减少乘法次数来实现提速，但是加法的数量会相应增加，也需要额外的变换计算及存储变换矩阵。随着卷积核和分块尺寸增大，需要考虑加法、变换和存储的代价，而且分块越大，变换矩阵越大，提效收益降低。

因此，Winograd适用于较小的卷积核和分块。

本文的部分内容、图片来源于：