本页目录

专业课复习

线性代数

介绍一下矩阵的秩，秩有什么物理意义？

从定义来说，矩阵的秩等于行向量组的秩，也就是行向量组中线性无关的向量的最大数目，对于列向量组同样成立，矩阵的行秩等于列秩。从几何意义来说，矩阵的秩是列空间或行空间的维度，也是线性变换后的空间维度。

向量组线性相关/线性无关的充要条件？

线性表示的角度：存在/不存在一个向量能被其他向量线性表示；
秩的角度：向量组的秩小于/等于向量个数；
线性方程组的角度：假设向量组记作 $A$ ，齐次方程组 $A X = 0$ 有/无非零解。

介绍下 $n$ 维向量空间？

一般地，由全体 $n$ 维向量构成的集合是 $n$ 维向量空间。集合对加法和数乘封闭。

什么是欧式空间？和向量空间是什么关系？

欧式空间是一个带有内积的向量空间，欧式空间是向量空间的一种特例。

线性方程组 $A X = b$ 的解有哪些情况，对应什么条件？

增广矩阵（也就是 $[A, b]$ ）的角度：
无解：消元后（增广矩阵的阶梯型）有 $0 =$ 非零常数的情况；
有唯一解：增广矩阵阶梯型非零行数等于未知数个数；
有无穷解：增广矩阵阶梯型存在零行。

空间变换/秩的角度：
无解：系数矩阵的秩小于增广矩阵的秩，或者 $b$ 不存在于向量空间 $A$ 中；
有唯一解：有解的前提下，系数矩阵或增广矩阵空间满秩（秩等于未知数个数）；
有无穷解：有解的前提下，系数矩阵或增广矩阵空间不满秩（秩小于未知数个数）。

假如非齐次方程组 $A X = b$ 有唯一解，那么齐次方程组 $A X = 0$ 解空间的维度是多少？

零维。

什么是矩阵特征值和特征向量？怎么求矩阵的特征值？特征值有什么物理意义？

定义： $n$ 阶方阵存在 $A X = λ X$ ，则数 $λ$ 为方阵 $A$ 的特征值，向量 $X$ 为属于 $λ$ 的特征向量。
求解： $f (λ) = ∣ λ I - A ∣ = 0$ 的 $n$ 个根就是 $n$ 个特征值， $k$ 重根对应至多 $k$ 个线性无关的特征向量。
物理意义：对于变换 $A$ 而言，特征向量 $X$ 只受拉伸作用，也就是变换前后共线，特征值 $λ$ 为拉伸倍数。

什么是代数重数和几何重数？二者有什么关系？

代数重数是特征值 $λ$ 在特征多项式中的重数，几何重数是特征值 $λ$ 对应的线性无关特征向量的个数。
代数重数 $\geq$ 几何重数。

矩阵相似的概念？相似矩阵有什么性质？相似矩阵有什么物理意义？

若存在可逆的 $n$ 阶方阵 $P$ ，使得 $P^{- 1} A P = B$ ，则称 $A$ 和 $B$ 相似。相似矩阵有相同的特征值、行列式、秩、迹，但不一定有相同的特征向量。相似是同一个线性变换在不同坐标系下的表达。

10.

矩阵可以相似对角化的充要条件是什么？

如果 $n$ 阶矩阵 $A$ 有 $n$ 个线性无关的特征向量，则 $A$ 可以相似对角化。

11.

特征值相同的矩阵一定相似吗？追加一个条件使得一定相似？

不一定。两者都可对角化（比如当这些特征值互异）时相似。

特征值有重根，不一定不可对角化；两个矩阵都不可对角化，也不一定不相似。

12.

什么是矩阵的迹，有什么性质？

方阵主对角线之和被称为矩阵的迹，记作 $t r (A)$ 。

转置不改变迹， $t r (A^{T}) = t r (A)$ 。

迹满足交换律，对于矩阵 $A_{n \times m}$ 与 $B_{m \times n}$ ，有 $t r (A B) = t r (B A)$ 。

迹等于特征值之和。（对特征多项式用韦达定理，此外还可得行列式等于特征值之积）

13.

矩阵合同的概念？

若存在可逆的 $n$ 阶方阵 $P$ ，使得 $P^{T} A P = B$ ，则称 $A$ 和 $B$ 合同。

14.

什么是正交矩阵，有什么性质？

$n$ 阶实矩阵满足 $A^{T} A = I$ ，则称 $A$ 为正交矩阵。此时有 $A^{- 1} = A^{T}$ 。
正交矩阵的行列式为 $\pm 1$ ，正交矩阵的乘积仍为正交矩阵。

15.

你觉得正交矩阵描述的空间变换具有什么几何性质？

正交变换不发生形变，只存在旋转和镜像操作。

16.

实对称矩阵有什么性质？

特征值都是实数，不同特征值的向量正交（对于普通矩阵仅仅是线性无关）。
对于实对称矩阵 $A$ 必然存在正交矩阵 $C$ 使得 $C^{T} A C = C^{- 1} A C = Λ$ ， $Λ$ 是对角阵。

主轴定理

对于一个实二次型 $f (X) = X^{T} A X$ ，总能通过正交变换 $X = P Y$ 使得：

f (X) = Y^{T} (P^{T} A P) Y = λ_{1} y_{1}^{2} + \dots + λ_{n} y_{n}^{2}

式中 $λ_{i}$ 是 $A$ 的特征值。

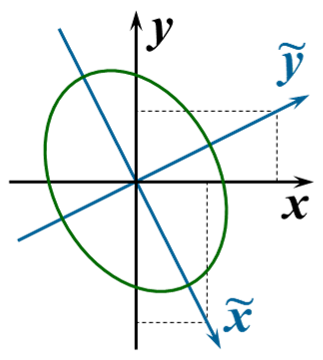
在二维情形理解其几何含义，也就是一个斜向的圆锥曲线可以正交变换为标准形式。

17.

介绍一下正定矩阵？

如果一个二次型对空间中任意 $X \neq = 0$ 都有 $f (X) > 0$ ，则其对应的矩阵 $A$ 为正定矩阵。（ $\geq 0$ 是半正定）

判断正定矩阵的充要条件有：特征值全部大于 $0$ 、顺序主子式全部大于 $0$ 等（注意前提是对称矩阵）。

概率论

介绍一下条件概率、全概率公式、贝叶斯公式。

条件概率： $P (B ∣ A) = \frac{P ( A B )}{P ( A )}$ 称为 $A$ 发生的条件下， $B$ 的条件概率。

全概率公式：如果 $A_{1} \dots A_{n}$ 是对事件空间的划分，有 $P (B) = \sum_{i = 1}^{n} P (A_{i}) P (B ∣ A_{i})$ 。

贝叶斯公式：条件同上，有 $P (A_{k} ∣ B) = \frac{P ( A _{k} ) P ( B ∣ A _{k} )}{P ( B )}$ 。贝叶斯公式可以理解为用先验概率 $P (A_{k})$ 估计后验概率 $P (A_{k} ∣ B)$ 。

说几个常见的离散型分布，它们的期望和方差是什么？

两点分布： $P (X = 0) = 1 - p$ ， $P (X = 1) = p$ ，有 $E (X) = p$ ， $D (X) = p (1 - p)$ ；

二项分布： $P (X = k) = C_{n}^{k} p^{k} (1 - p)^{n - k}$ ，有 $E (X) = n p$ ， $D (X) = n p (1 - p)$ ；可以理解为进行 $n$ 次实验，事件发生次数的可能情况；

泊松分布： $P (X = k) = \frac{λ ^{k}}{k !} e^{- λ}$ ，有 $E (X) = D (X) = λ$ ；泊松分布是二项分布 $n \to \infty$ 、 $p$ 很小时的极限情况。

方差的公式是什么，有什么变形？

$D (X) = E (X - E (X))^{2} = E (X^{2}) - E (X)^{2}$ 。

协方差的公式是什么，有什么变形？

$co v (X, Y) = E [(X - E (X)) (Y - E (Y))] = E (X Y) - E (X) E (Y)$ 。

协方差和相关系数是什么关系？

$X$ 与 $Y$ 的相关系数是它们经过标准化之后的协方差。

ρ = co v (X^{*}, Y^{*}) = \frac{co v ( X , Y )}{D X D Y}

$X \pm Y$ 的方差怎么求？

如果 $X$ 与 $Y$ 独立， $D (X \pm Y) = D (X) + D (Y)$ ；
更一般的情况是： $D (X \pm Y) = D (X) + D (Y) \pm 2 co v (X, Y)$ 。

解释一下相关和独立和关系，判断条件是什么？

独立一定不相关，但不相关不一定独立。独立是完全无关，而统计学上的相关一般指线性相关。

$A$ 和 $B$ 独立的充要条件是 $P (A B) = P (A) P (B)$ ； $A$ 和 $B$ 的协方差/相关系数不为 $0$ 就相关。

什么是依概率收敛？

依概率收敛是指对于任意 $ϵ > 0$ ，有 $P (∣ X_{n} - X ∣ > ϵ) \to 0$ ，则称 $X_{n}$ 依概率收敛到 $X$ 。

介绍一下大数定律？

如果随机变量序列 $X_{1}, X_{2}, \dots, X_{n}, \dots$ 满足

\frac{1}{n} \sum_{i = 1}^{n} X_{i} \to P \frac{1}{n} \sum_{i = 1}^{n} E (X_{i})

则称 ${X_{n}}$ 服从大数定律。

大数定律刻画了随机变量的平均值依概率收敛为期望的均值。

切比雪夫大数定律：如果 ${X_{n}}$ 两两不相关，且方差有限，则 ${X_{n}}$ 服从大数定律。

伯努利大数定律：如果事件 $A$ 在 $n$ 次伯努利试验中发生了 $n_{A}$ 次，事件 $A$ 发生的概率为 $p$ ，则有 $\frac{n _{A}}{n} \to P p$

辛钦大数定律：如果 ${X_{n}}$ 独立同分布，且期望存在，则 ${X_{n}}$ 服从大数定律。

伯努利大数定律意义是频率估计概率；上面提到的另外两个大数定律意义是均值估计期望，但条件有所不同。

10.

介绍一下中心极限定理？

大数定律研究一系列随机变量 ${X_{n}}$ 的均值 $\overset{ˉ}{X}_{n}$ 是否收敛于期望，而中心极限定理进一步研究了 $\overset{ˉ}{X}_{n}$ 的分布。

若 ${X_{n}}$ 满足一定的条件，当 $n$ 足够大时， ${X_{n}}$ 近似服从正态分布，这就是中心极限定理的主要思想，这也体现了正态分布的重要性与普遍性。

独立同分布中心极限定理：设 ${X_{n}}$ 是独立同分布的随机变量序列，期望为 $μ$ ，方差为 $σ^{2}$ ，则有 $n$ 足够大时 $\overset{ˉ}{X}_{n}$ 近似服从正态分布 $N (μ, \frac{σ ^{2}}{n})$ 。

11.

正态分布的和/差的分布是什么？

如果 $X \sim N (μ_{1}, σ_{1}^{2})$ ， $Y \sim N (μ_{2}, σ_{2}^{2})$ ，且 $X$ 与 $Y$ 独立，则 $X \pm Y \sim N (μ_{1} \pm μ_{2}, σ_{1}^{2} + σ_{2}^{2})$ 。

12.

计算方差时，什么时候要除以 $n$ ，什么时候要除以 $n - 1$ ？

如果有总体的数据，除以 $n$ 即可；如果数据是总体抽出的 $n$ 个样本，计算方差要除以 $n - 1$ ，这被称为样本方差。

13.

计算样本方差时，为什么要除以 $n - 1$ ？

为了保证样本方差是对总体方差的无偏估计。

14.

极大似然估计是什么？

如果已知了分布的形式，用能够最大化观测到当前样本的概率的参数值，作为对分布参数的估计值。

追问：如果不知道分布的形式怎么办？

模式识别非参数估计：直方图，k近邻，Parzen窗。

计算机网络

网络为什么要分层呢？分哪些层？每层的职责是什么？

计算机科学领域的很多问题都通过分层来解决，设计层次结构的主要目的是将复杂的问题划分为较小的、较为清晰的问题，各层之间相互独立，从而上层可以利用下层抽象出来的接口，而不用关心下层的具体实现。

自底向上有：
物理层：为数据比特传输提供物理媒介。
链路层：数据在链路层分装为帧，链路层负责帧在相邻节点之间的可靠传输，服务于网络层。
网络层：网络层传输IP数据报，将源节点发出的数据包传送到目的节点，提供主机之间点到点的传输。
运输层：运输层为主机的进程之间提供端到端的服务。
应用层：提供特定应用的网络服务。

你电脑上发出去的数据，先被运输层包装，还是先被网络层包装？

先被运输层包装。对于发送方而言，从上到下层层包装；对于接收方而言，从下到上层层解开包装。

介绍一下奈奎斯特定理和香农定理？

奈奎斯特定理：理想低通信道，极限数据传输速率为 $2 W lo g_{2} V$ (bit/s)，其中 $W$ 为信道带宽(Hz)， $V$ 为码元的离散电平数目。
（例如， $4$ 位码元 $V = 16$ ）
也可以表述为：理想低通信道，最高码元传输速率为 $2 W$ (码元/s)。

香农定理：在有噪声的信道中，信息传输的极限速率为 $C = W lo g_{2} (1 + \frac{S}{N})$ (bit/s)，其中 $W$ 为信道带宽(Hz)， $\frac{S}{N}$ 为信噪比。

码元传输速率超过上限会发生什么？

码间串扰，即失去码元之间清晰的界限。

媒体接入控制是什么？有哪些方式？

当多个发送方和多个接收方共享一个信道时，需要协调对这个信道（物理媒介）的访问，这也是媒体接入控制旨在解决的问题。

媒体介入控制大体可以分为两种：静态划分信道和动态接入控制，前者也就是多路复用技术，包括时/频/波/码分多路复用；后者通过协议来进行控制。
动态接入控制又可以分为轮询访问和随机访问，轮询访问有令牌传递协议；随机访问包括ALOHA、CSMA、CSMA/CD、CSMA/CA协议等。

CSMA/CD中文是什么？CSMA/CD相比CSMA有什么区别？

CS：载波监听；MA：多路访问；CD：碰撞检测。
CSMA发生冲突仍然会把数据帧发完，等待接收方响应NAK（或不响应），这是一种被动的方式。CSMA/CD则是主动检测到冲突后立即停止发送，等待随机时间（截断二进制指数回退）后再次发送。

再介绍一下CSMA/CA？

CA：碰撞避免。CSMA/CA用于无线网络。无线网络存在“隐蔽站”问题，使用碰撞检测意义不大；CSMA/CA通过预约信道机制实现碰撞避免。考虑到无线信道通信质量远不如有线信道，CSMA/CA使用确认帧机制。

介绍一下争用期的概念，争用期有什么意义？

争用期是 $2$ 倍的单程传播时延。如果经过争用期时间，还没有检测到碰撞，就一定不会发生碰撞。

解释一下以太网为什么要限制最小帧长和最大帧长？（可以不给出精确数字，只定性的解释原因）

限制最小帧长：帧的传输时间要大于争用期，防止一个站点还没来得及检测到其发送的帧产生了碰撞，就已经将这个帧发送完毕了。
限制最大帧长：防止一个站点过长时间的占用信道；同时也是防止接收方的缓冲区产生溢出。

10.

交换机和路由器的区别？

交换机工作在链路层，根据MAC地址转发数据；路由器工作在网络层，根据IP地址转发数据。

11.

MAC地址和IP地址有什么区别？

MAC是链路层地址，IP是网络层地址；
MAC地址具有唯一性，IP地址不具有。

12.

介绍你知道的动态路由协议？

RIP：属于内部网关协议，基于距离矢量法，使用UDP；RIP协议只和相邻路由器交换信息，交换的信息是自己的路由表。
OSPF：属于内部网关协议，基于链路状态法，使用IP；路由信息会泛洪给网络中所有路由器，每个路由器计算以自身为根节点到所有节点的最短路径树。OSPF相比于RIP更适用于大型网络。
BGP：属于外部网关协议，使用TCP。负责自治系统之间的路由选择。

13.

怎么判断一个子网掩码是否合法？

二进制32位，且满足形式：连续的1后面跟随连续的0。

14.

有没有可能一个主机的公网IP地址是192.168.3.3？

不可能。192.168.0.0~192.168.255.255被用作为私有地址，仅对本地网络中的设备有意义。想在互联网上发送或接收数据需要用到NAT。

追问：介绍一下NAT协议？

全称是网络地址转换。NAT可以将内网的IP地址映射到互联网上的IP地址，从某种角度，NAT使得路由器对外界隐藏了本地网络的细节。

15.

升级到IPv6主要是为了解决什么问题？IPv6比IPv4有什么改进？

为了解决IPv4地址用尽。IPv6地址空间更大，且改进了报文头（例如移除了校验和字段、可选字段）以提高路由效率。

16.

介绍一下ARP协议？

全称是地址解析协议。ARP协议用于解决在同一个局域网中，已知IP地址，如何找到对应的MAC地址。ARP协议维护一个IP地址和MAC地址的映射表，如果在ARP表中找不到对应的IP地址，就会广播ARP请求，请求对应IP地址的主机回复自己的MAC地址。

17.

介绍一下ICMP协议？

全称是互联网控制报文协议。ICMP是网络层协议，从技术角度来说就是一个差错报告机制，不用来传递数据，而是用作网络诊断、排除故障等。一个常见的应用是ping命令。ICMP协议可能被恶意的用作拒绝服务攻击。

18.

介绍一下DHCP协议？

全称是动态主机配置协议。DHCP是使用UDP协议的应用层协议，用于自动给内网设备分配IP地址。分为发现、提供、选择、确认四个阶段。

19.

说说TCP和UDP的区别？

TCP是面向连接的，UDP是无连接的；
TCP提供可靠数据传输，UDP是不可靠的；
TCP资源负载比较大，由于有流量控制、拥塞控制等机制，TCP比UDP慢。

20.

介绍一下TCP连接建立、释放的过程？

连接建立：三次握手，客户端请求，服务端确认，客户端再次确认。

连接释放：四次挥手，客户端请求，服务端确认，服务端发送完全部数据后发送连接释放报文，客户端收到后确认。
客户端确认了连接释放报文段后，还要经过二倍MSL时间才能关闭连接，以防发送的确认报文丢失。如果直接进入关闭状态就无法接收到服务端重传的连接释放报文。

追问：为什么建立连接不能两次握手？

TCP是双向通信协议，双方都分别需要通过一次SYN和一次ACK来约定序列号等参数，保证连接的可靠性。虽然这样看起来是四步，但实际上中间的两次（服务端响应客户端的ACK、服务端请求客户端的SYN）是合并到一起的，因此总共需要三次握手。

另一个角度：如果客户端发送了两个连接请求（第一个连接请求因为网络原因延迟到达），可能延迟到达的请求被收到时，最开始的连接已经释放了。如果服务端不需要第三次握手，就会直接进入连接状态，但是又收不到客户端发送的数据，导致资源浪费。

21.

TCP是怎么保证可靠传输的？

TCP的发送方会维护发送窗口，接收方也会维护接收窗口，这点与SR类似；但TCP采用与GBN类似的累计确认。需要注意的是，GBN中ACK n表示序号为n及其之前的分组都已经被正确接收，而TCP中ACK n表示序号为n-1及其之前的分组都已经被正确接收，接收方期望收到的最小序号的分组是序号n。

22.

TCP是怎么做流量控制和拥塞控制的？二者的异同？

流量控制：为了防止发送方传输速度超过了接收方的接收能力。接收方通过设置头部中的窗口字段，根据自己接收缓存的大小，动态地调整发送方的发送窗口大小。

拥塞控制：为了防止过多数据注入到网络当中。手段有：慢开始、拥塞避免、快重传、快恢复。

流量控制是端到端的问题，由接收方主动控制发送方的发送窗口，受限于接收方接收能力；拥塞控制是网络上的全局问题，由发送方主动控制发送速率，受限于网络拥塞程度。相同点是二者控制的对象都是发送方的发送速率。

追问：详细介绍一下拥塞控制的手段？

慢开始：拥塞窗口从1开始指数增长到门限值。

拥塞避免：增大到门限值后线性加1，如果发生了超时重传，将门限设为当前拥塞窗口的一半，然后将拥塞窗口置1。

快重传：收到三次重复的ACK n，就不等待重传计时器了，立即重传分组n。

快恢复：配合快重传使用。如果发生了快重传，就知道现在只是丢失了个别的报文段而不是网络拥塞。于是不启动慢开始算法，将当前拥塞窗口减半，并把门限设为此值。然后执行拥塞避免算法。

编程语言

堆和栈的区别？

二者各有利弊：栈的内存分配更快，但只能对堆顶操作；堆允许随机分配和释放，但会带来更大的开销。

堆区：由人为分配/释放；效率更慢；
栈区：由编译器自动分配/释放；效率更快；栈区的大小在程序编译时确定，通常比较小。

C++的new和malloc有什么区别？

new会在堆区新建对象，并返回对象的指针，会调用构造函数；
malloc只是在堆区分配内存，并不会初始化，返回值也是void*类型，需要对返回值做强制类型转换。

#include <iostream>
using namespace std;
struct POINT {
    int x,y;
    POINT(int x=10,int y=10):x(x),y(y)
    {
        cout<<"create point("<<x<<","<<y<<")\n";
    }
    ~POINT()
    {
        cout<<"destruction!";
    }
};
int main()
{
    POINT *p1=new POINT;//create point(10,10)
    cout<<p1->x<<' '<<p1->y<<endl;//10 10

    POINT *p2=(POINT*)malloc(sizeof(POINT));
    cout<<p2->x<<' '<<p2->y<<endl;//12348784 0

    delete(p1);//destruction!
    free(p2);
    return 0;
}

C++的指针和引用有什么区别？

指针是一个变量，其值是一个地址；可以有多级；指针可以重复赋值；指针可以为空。
引用是一个已经存在的变量的别名；只能有一级；引用不可以重新绑定到其他变量；引用不可以为空。

杂题

只能用加、减、乘、除、乘方、开方六则运算， $x, y > 0$ ，怎么从数学上近似表示 $max (x, y)$ 和 $min (x, y)$ ？

lim_{n \to \infty} (x^{n} + y^{n})^{1/ n} = max (x, y)

lim_{n \to - \infty} (x^{n} + y^{n})^{1/ n} = min (x, y)

说说你接触/听说过的研究方向，有哪些顶会顶刊？

计算机视觉：CVPR、ICCV、ECCV、TPAMI（顶刊）
机器学习：ICML、ICLR、NIPS
自然语言处理：ACL、NAACL、EMNLP
安全：ACM CCS、NDSS、USENIX Security、IEEE S&P

你怎么理解计算机网络中的可靠传输？

可靠传输服务希望实现发送端发送什么，接收端就接收到什么。希望解决数据位出错、分组丢失、分组失序、分组重复等错误。

你怎么理解计算机网络中的“即插即用”一词？

意味着无需人工，具有自动配置的能力。

追问：那你觉得计算机网络中什么是即插即用的？

交换机是即插即用的，插上网线就能自动学习MAC地址，不需要配置。
ARP是即插即用的，ARP表是自动建立的，不需要系统管理员来配置；
DHCP是即插即用的，能够实现自动分配IP地址。
IPv6是即插即用的，支持无状态地址自动配置，不需要DHCP。

家里的路由器的WAN口和LAN口分别接什么？光猫怎么接？

WAN(Wide Area Network)口接外网，LAN(Local Area Network)口接内网，也就是家里的设备。事实上如果不接WAN口，路由器就变成了交换机。

光猫的原理是将光信号转换为电信号，接入光纤，输出电信号给路由器。光猫应该接在路由器和外网之间，因此要接路由器的WAN口。