【GAMES101】Geometry

几何的隐式和显式表示

隐式：$x^2+y^2+z^2-1=0$

显式：$(u,v)\to (\cos u\sin v,\sin u\sin v,\cos v)$

隐式(implicit)表示就像数学中的隐函数，比如$f(x,y)=0$、$g(x,y,z)=0$，通过描述点满足的条件来表达几何体；这样的方式容易验证一点$(x_0,y_0,z_0)$是否在定义的面上，但求出构成形体的所有点是困难的，因为这需要求出方程的解。

显式(explicit)表示通过参数映射的方式，例如在3D空间中定义$f:{\mathbb{R}}^2\to {\mathbb{R}}^3$来描述一个几何体。这样求出构成几何体的点是容易的，只需要遍历函数定义域；但验证一点是否在表面上是困难的。

更多隐式表示

代数曲面

如前面所说的，代数曲面(Algebraic Surfaces)用数学公式来表达几何体。这种方法很难表示复杂的形体。

构造实体几何 - CSG

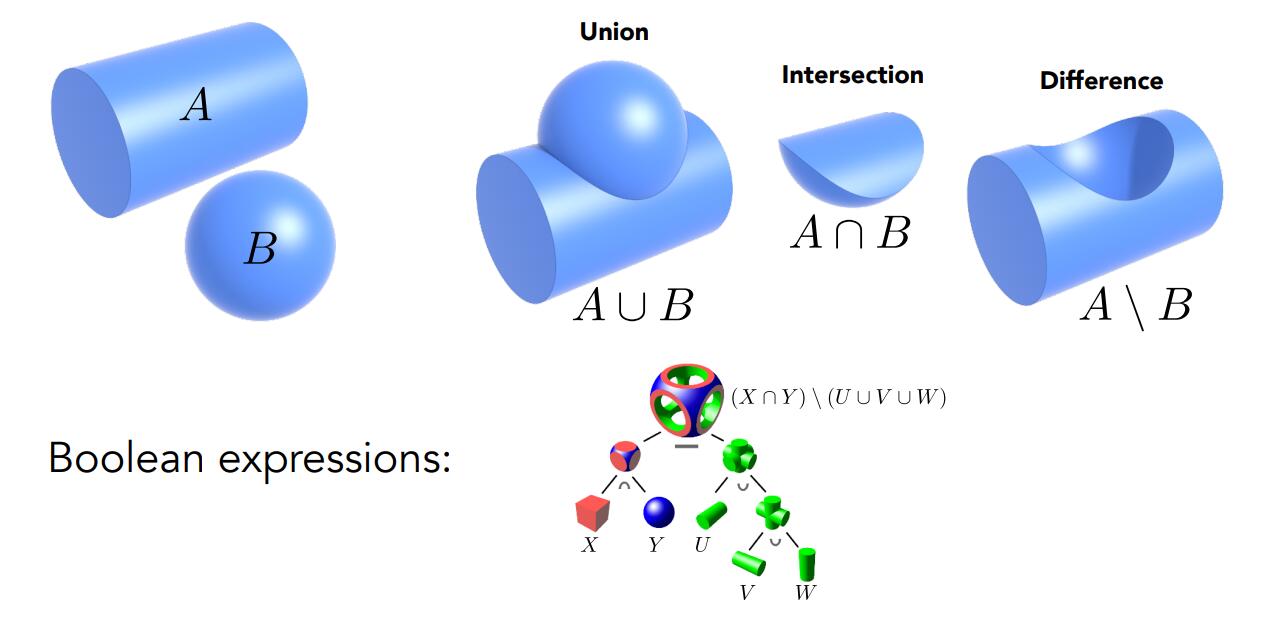
构造实体几何(Constructive Solid Geometry, CSG)通过基本几何体的布尔运算（交、并、差等）来定义新的几何体。

有符号距离函数 - SDF

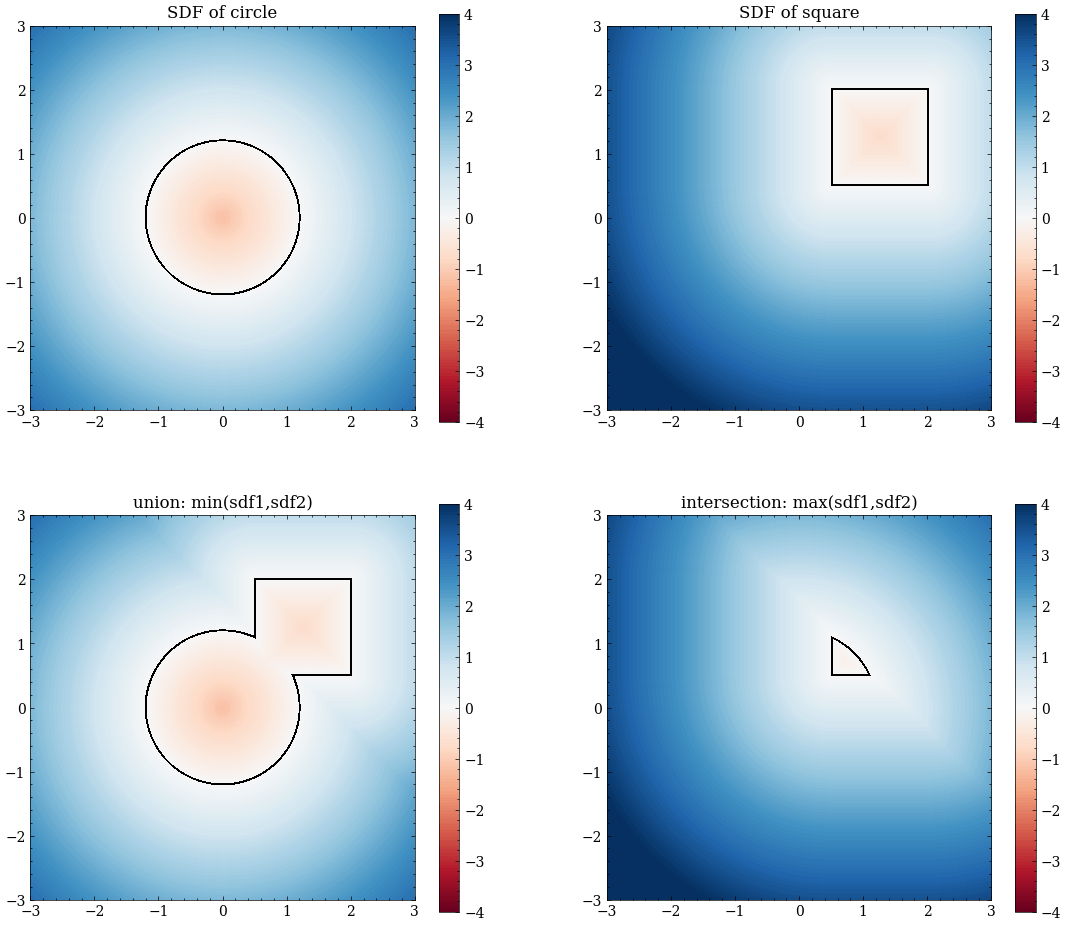
有符号距离函数(Signed Distance Function, SDF)定义空间中一点到要描述的表面的最短距离，如果点在物体内部，则这个距离取负数。

合并和相交

通过对两个SDF函数的运算，得到一个新的SDF函数，再求出这个新SDF函数值为$0$的部分，即可得到组合后的图形。

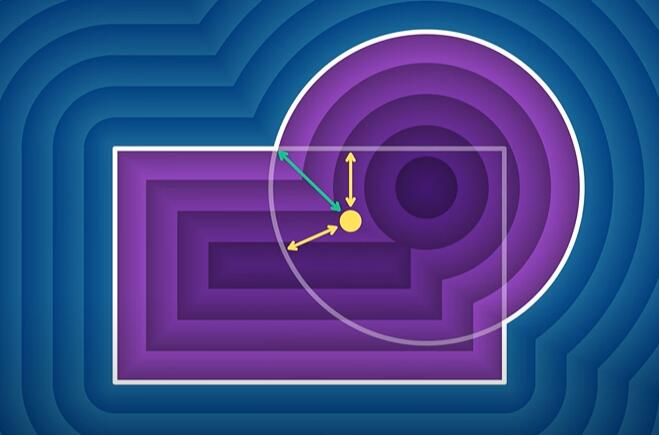
要注意的是，这个结果并不是完全准确的，例如下图中的黄点的组合SDF值为两条黄色线段的最小值，但其准确值应为绿色线段的长度。出现这个问题的原因是，计算得到原图形SDF值的边界在新图形中已经不存在了。不过在应用中我们可以忽略这个小问题。

混合

给两个图形的SDF函数加权相加可以实现混合(blending)效果。

分形

分形(Fractals)具有自相似性。

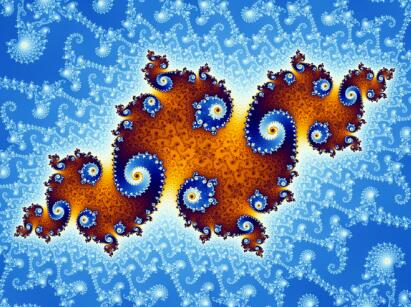
分形的变化频率非常高，在渲染时会引发强烈的走样。

更多显式表示

点云

点云是最简单的表示方法，用列表存储各个点的信息。只要采样足够密集，理论上可以表示任何几何体。

多边形

图形学中最广泛的应用通常是三角形面。

Wavefront Object (*.obj) 文件简介

这是Wavefront科技开发的一种描述三维对象的文件格式，是一个文本文件，通常包含顶点v，法线vn，面f等定义信息；例如下面的代码表达了一个四面体：

# 顶点
v  1.0  1.0  1.0
v -1.0 -1.0  1.0
v -1.0  1.0 -1.0
v  1.0 -1.0 -1.0

# 面
f 1 2 3
f 1 3 4
f 1 4 2
f 2 4 3

f后面是顶点的索引。更详细的资料可以参考维基百科。

网站ONLINE 3D VIEWER可以在线查看各种格式定义的3D模型。

贝塞尔曲线

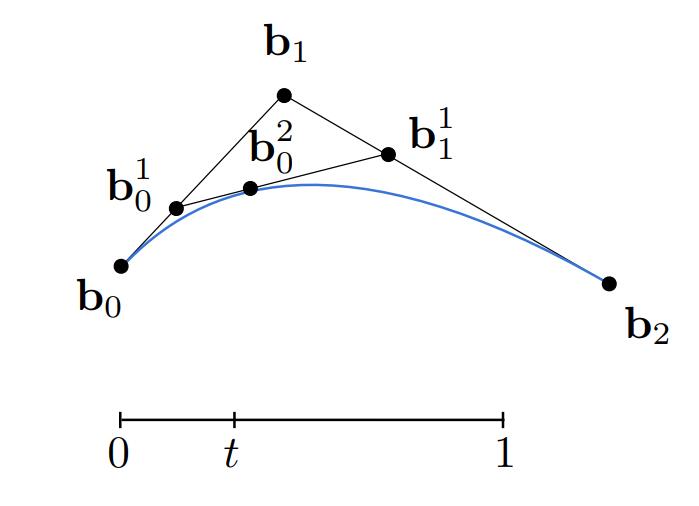
我们可以通过三个控制点$b_0$、$b_1$、$b_2$来生成图中蓝色的曲线，具体做法是对于每个$t\in [0,1]$：
做出点$b_0^1$、$b_1^1$，满足$b_0{b}_0^1=t{b}_0{b}_1$、$b_1{b}_1^1=t{b}_1{b}_2$；
再做出$b_0^2$，满足$b_0^1{b}_0^2=t{b}_0^1{b}_1^1$；

每一个$t$对应的$b_0^2$就构成一条贝塞尔曲线，也就是图中蓝色的曲线。

三阶贝塞尔曲线

如果用四个控制点，同样通过类似的递归的方法，可以生成一条更高阶的贝塞尔曲线：

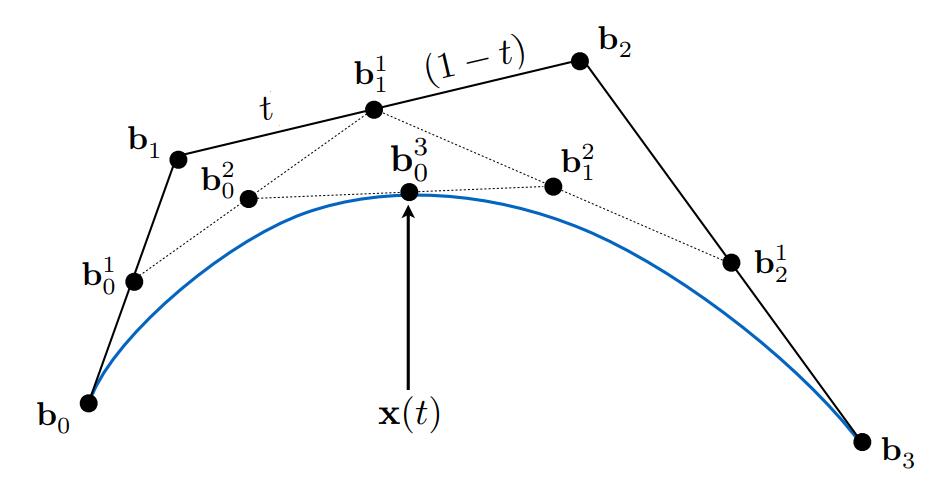
对于三阶贝塞尔曲线上一点$b_0^3$，也就是图中标识的$x(t)$，尽管从演示上是通过中间点一步一步得到的，但实际给出四个控制点位置和$t$就可以唯一确定。

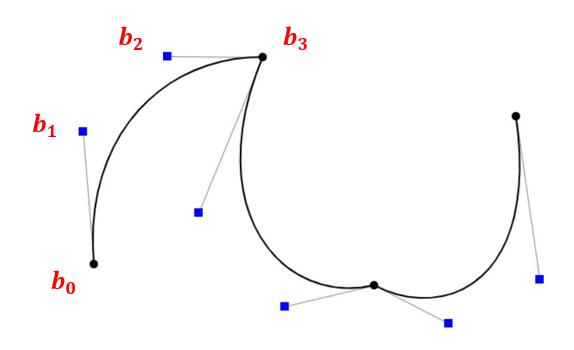
下图中左侧是常见的分段定义贝塞尔曲线的方法，每个顶点都延伸出两根“控制杆”，而实际上三阶贝塞尔曲线的四个控制点是图中标出的$b_0$~$b_3$，相当于省去了连线$b_1{b}_2$。

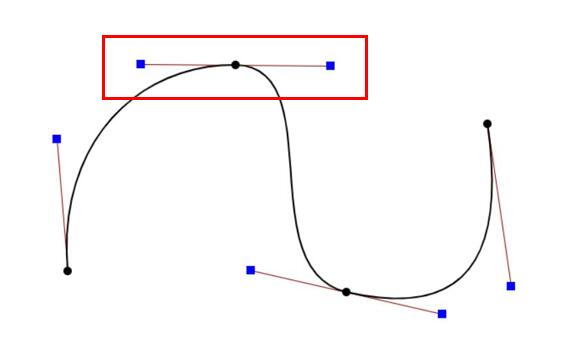
如果希望分段贝塞尔曲线连续，则需要两侧的“控制杆”反向共线且等长，如下图中右侧所示。

这个网站可以在线编辑贝塞尔曲线。

贝塞尔曲面

描述一维贝塞尔曲线时需要一个参数$t$，自然地，对于贝塞尔曲面需要两个参数$u\in [0,1]$,$v\in [0,1]$。

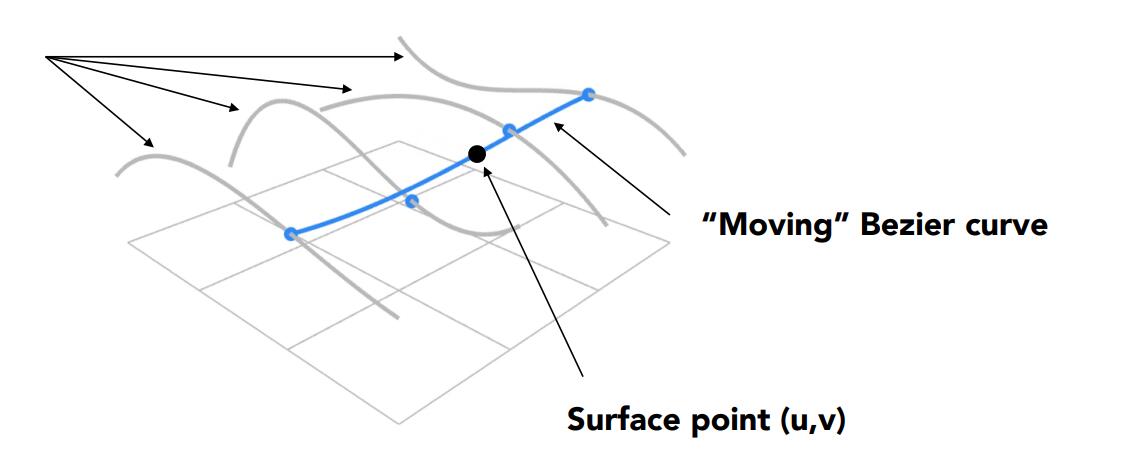
生成贝塞尔曲面的方式类似双线性插值：我们需要16个控制点排列成$4\times 4$，对于四个点组成的一列可以生成一个贝塞尔曲线（图中灰色线），指定了参数$u$后，可以分别得到四条曲线上的四个点（图中蓝色点）；以这四个蓝色点作为新的控制点，每一个参数$v$都会给出蓝色贝塞尔曲线上的一点（图中白色点）。

这就是参数$(u,v)$到贝塞尔曲面上一点的一一对应关系。

网格操作

网格细分

网格细分(mesh subdivision)相当于上采样，可以增加分辨率。

Loop细分

Loop细分可以概括为两步操作：

其中第二步对于“新的”（新取的中点）顶点和“老的”（原本就有的）顶点更新方式分别为：

新的顶点位置调整为周围四个点位置的加权平均：$3(A+B)/8+(C+D)/8$

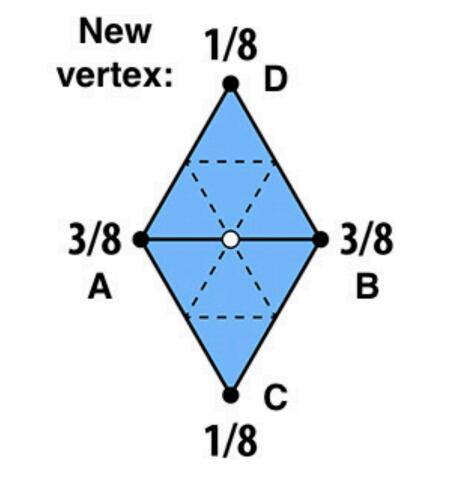
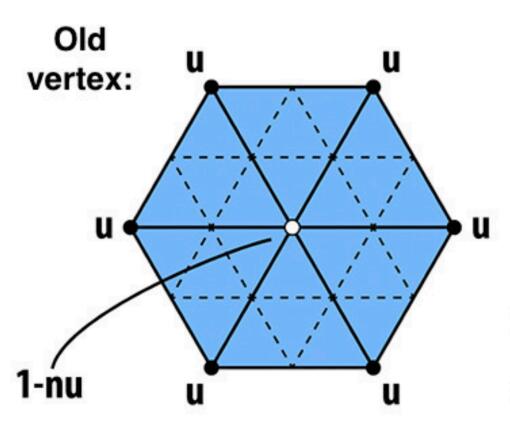
对于旧的顶点，其位置调整为自己原本位置与所有邻居的加权平均：
$(1-nu)p_{original}+u\sum p_{neighbor}$

其中$n$是节点的度数，$n=3$时$u=3/16$，其他情况下$u=3/8n$。

Catmull-Clark细分

Catmull-Clark细分针对四边形网格，同样的可以概括为两步操作：

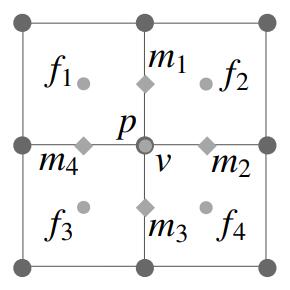
对于四边形面中心点，其取法为：$f=\frac{v_1+v_2+v_3+v_4}{4}$

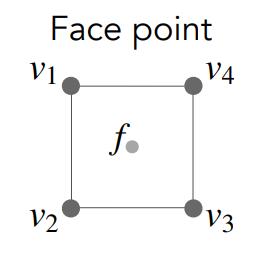
对于边点，其取法为：$e=\frac{f_1+f_2+v_1+v_2}{4}$

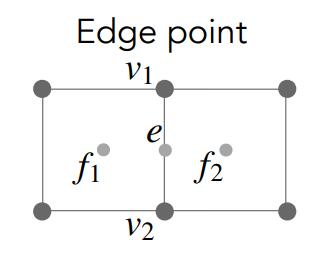
第二步，对于原来的顶点$p$，其调整为：$v=\frac{f_1+f_2+f_3+f_4+2(m_1+m_2+m_3+m_4)+4p}{16}$
这里的$m$是边的中点，与上面求得的边点不同。

网格简化

网格简化(mesh simplification)相当于下采样。

边坍缩

边坍缩合并一条边的两个顶点。

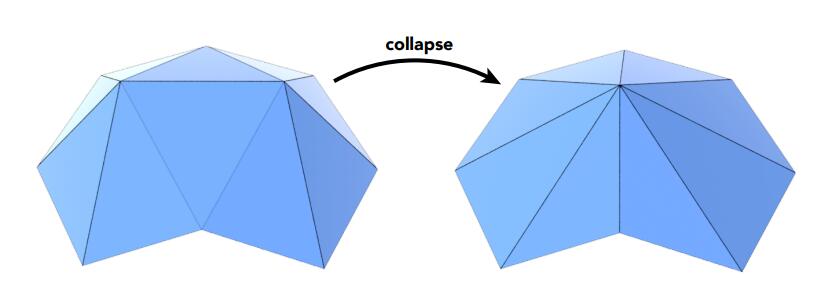
如何评定新的顶点与原模型轮廓一致的程度呢（例如下面左图取平均的效果明显不如右图）？答案是优化⼆次误差，也就是新的顶点与原来的各面的距离平方之和最小。

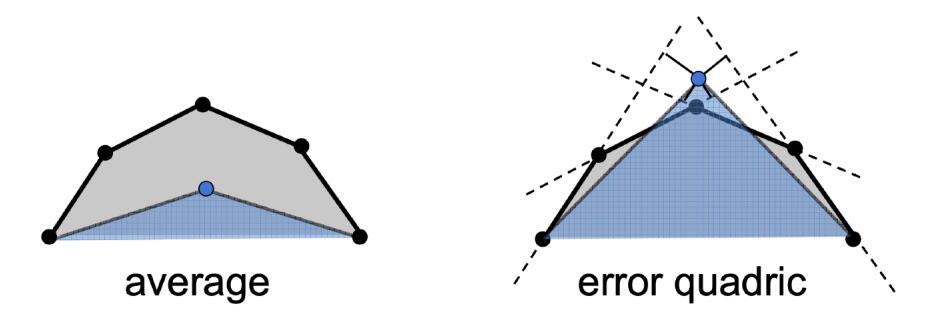
执行算法时，对于模型的每一条边，都可以算出坍缩后最优的⼆次误差；使用贪心算法，每次取二次误差最小的边进行坍缩。注意到，将一条边坍缩后，会影响与这条边相邻接的其他边的位置，自然也会影响其他边的最优二次误差值，因此每次操作后还需要调整部分边的最优二次误差值。可以利用优先队列实现功能。