【GAMES101】Rasterization

在2D屏幕上显示物体时，最终的图像是由一个一个像素构成的。光栅化需要解决的问题就是将连续的物体表示离散化。

为什么使用三角形

三角形在图形学中广泛应用，是因为其具有一些良好的性质：

采样

最朴素的想法是：对于一个像素，考虑它的中心点是否在给定的三角形内。如果在，像素值就为1，否则为0。如图：

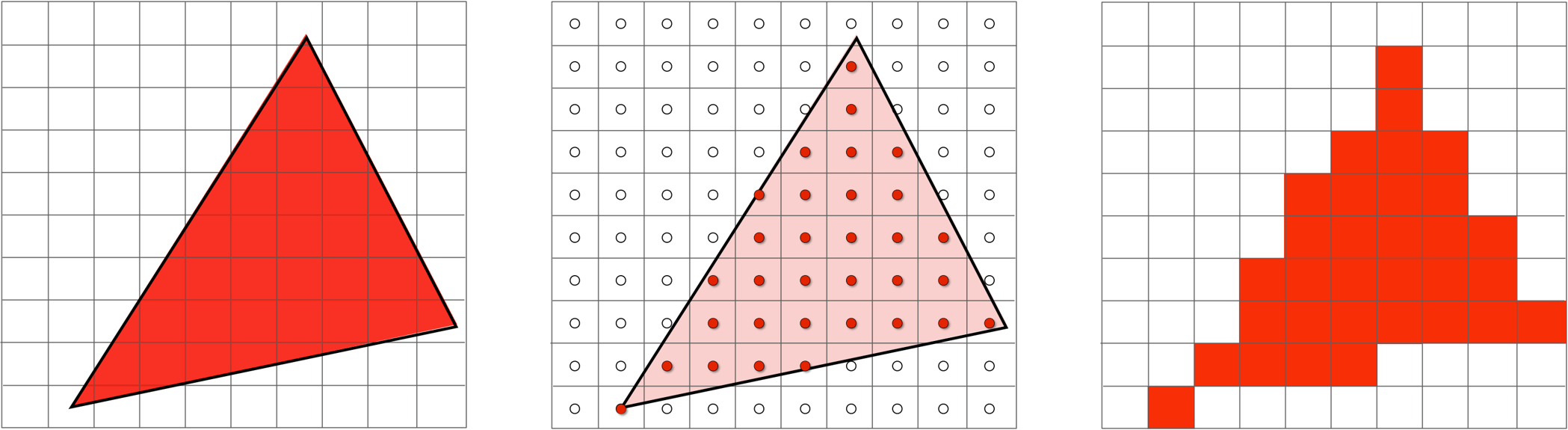
判断一点是否在三角形内使用如下方法：

首先，来判断$Q$点在$P_1{P}_2$的哪侧，这可以由向量叉乘$P_1{P}_2\times P_{1}Q$的符号得到，在右手系中这是一个指向屏幕外的向量。

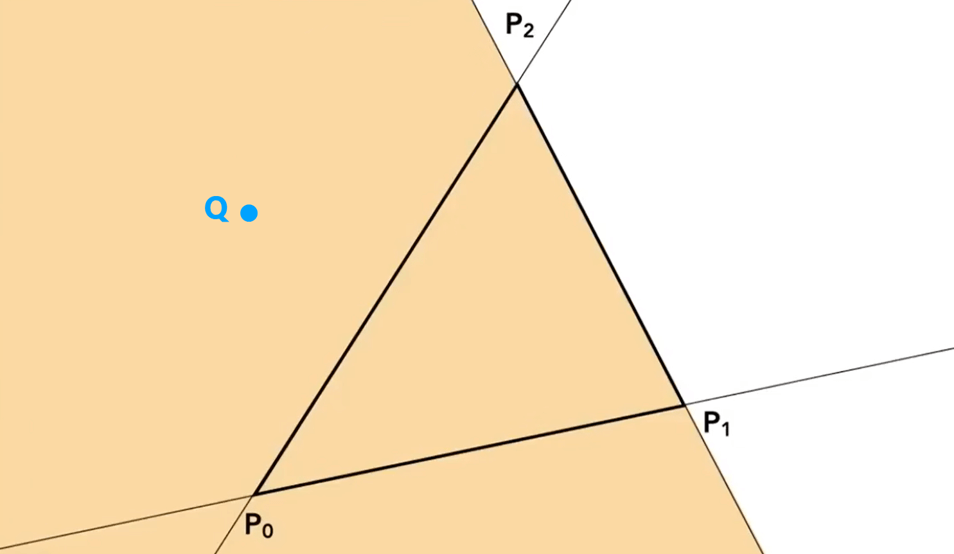
根据这个原理，如果$P_0{P}_1\times P_{0}Q$、$P_1{P}_2\times P_{1}Q$、$P_2{P}_0\times P_{2}Q$的符号相同，就说明$Q$点同时在三角形三条边的同侧，唯一的情况就是$Q$点在三角形内部。

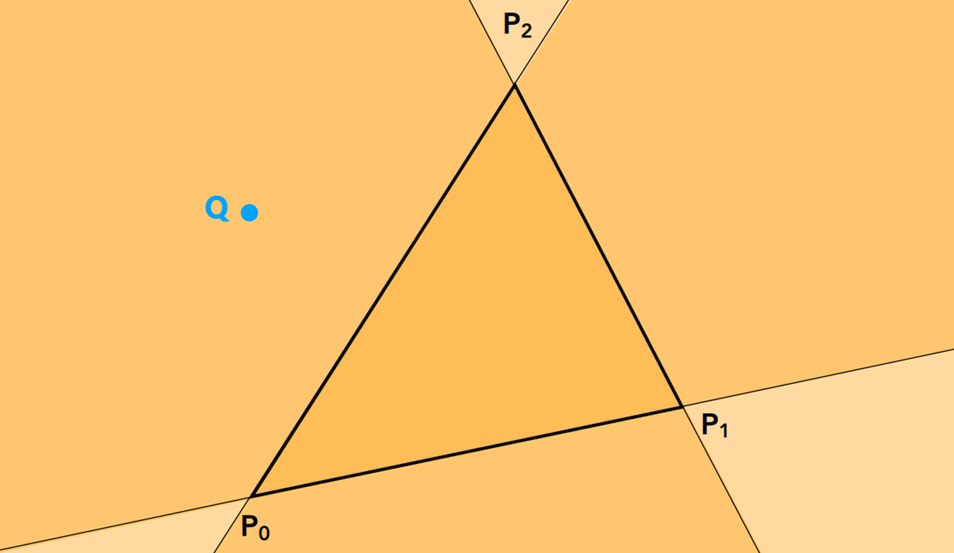
对于下图所示情况，假如我们规定指向屏幕外为正方向，会发现$P_2{P}_0\times P_{2}Q$符号为负，其余为正，不满足符号相等的条件，因此判断其在三角形外部。

采样的问题

采样的问题是会产生锯齿(jaggies)，出现走样(aliasing)。

反走样

反走样(Anti-Aliasing)也叫抗锯齿，核心的想法是先模糊，再采样。笼统的来说，这样做可行的原理是：直接采样效果不好是因为信号的高频部分超过了采样的频率。对于图像来说，高频的部分通常是边缘；如果能通过模糊充当低通滤波的操作，就可以改善因为采样频率不足带来的失真。

SSAA

超采样反走样(Super-Sampling Anti-Aliasing, SSAA)通过对每个像素取多次采样，直接提高了采样率；最后的结果是所有采样点颜色取平均。

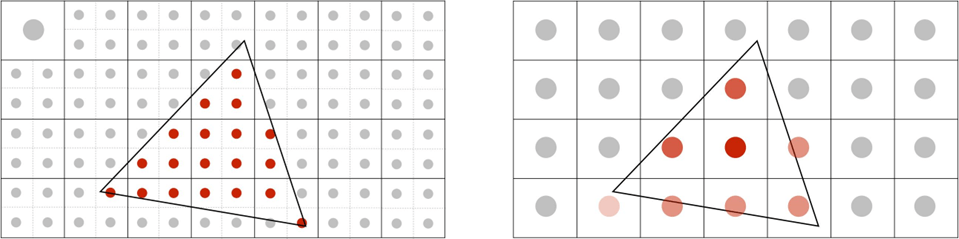
MSAA

多重采样反走样(Multi-Sampling Anti-Aliasing, MSAA)是对SSAA的改进：MSAA不再对每个采样点进行单独的着色，而是对每个像素只执行一次着色计算，从而降低了计算量。

Z-Buffer

在这节我们约定$z$为正数，且更小的$z$值代表更近的像素点。

深度缓冲记录每一个像素的深度信息。当渲染三维场景时，将每个像素的深度值与Z-Buffer中相应位置的值进行比较，如果当前像素的深度值更小，则更新Z-Buffer中的值并将当前像素的颜色值渲染到屏幕上。