本页目录

【GAMES101】Transformation

null likes · null views · 2024-01-07

2D变换

缩放 Scale

[x^{'} y^{'}] = [s_{x} 0 0 s_{y}] [x y]

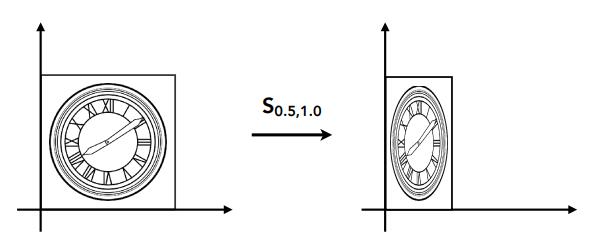
切变 Shear

[x^{'} y^{'}] = [10 a 1] [x y]

$y = 0$ 时水平偏移是 $0$

$y = 1$ 时水平偏移是 $a$

垂直偏移总是 $0$

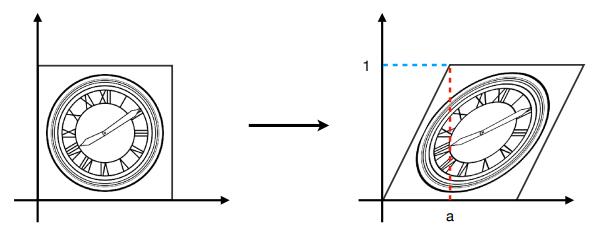
旋转 Rotate

R (θ) = [cos θ sin θ - sin θ cos θ]

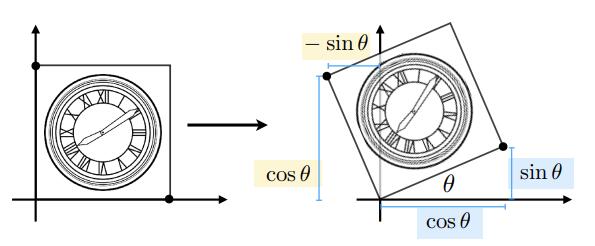
平移 Translation - 引入齐次坐标

下面这个简单的平面平移变换并不能用2维矩阵表示：

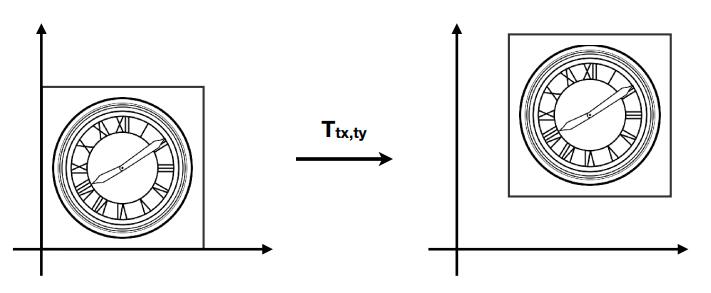
引入齐次坐标

我们不希望将平移操作看待为一个特例，而是想要找到一个统一的、适用于各种变换的方法。
这个解决方案就是引入齐次坐标Homogeneous Coordinates：

现在我们用3个维度来表示一个2D的点或向量：

2D点： $(x, y, 1)^{T}$

2D向量： $(x, y, 0)^{T}$

理解最后一个维度

对于点和向量的运算，下表的结论是显然成立的：

运算	结果
向量 + 向量	向量
点 - 点	向量
点 + 向量	点
点 + 点	无意义

通过最后一个维度是 $1$ 或 $0$ 分别表达点或向量，可以满足上述性质。

此时平移变换就可以表示为：

x^{'} y^{'} 1 = 100010 t_{x} t_{y} 1 x y 1 = x + t_{x} y + t_{y} 1

在齐次坐标下，前面提及的变换都可以表示为矩阵

a c 0 b d 0 t_{x} t_{y} 1

组合变换

组合变换的矩阵顺序会影响结果，应该从右至左结合。
对于一点 $x = (x, y, 1)^{T}$ 先应用 $A_{1}$ ，再应用 $A_{2} \dots$ ，最后应用 $A_{n}$ ，应该写为：

A_{n} \dots A_{2} A_{1} x

3D变换

一般形式

由2D变换推广而来，在齐次坐标下3D变换的一般形式可以表示为：

x^{'} y^{'} z^{'} 1 = a d g 0 b e h 0 c f i 0 t_{x} t_{y} t_{z} 1 x y z 1

3D旋转

绕坐标轴旋转

R_{x} (θ) = 1000 0 cos θ sin θ 0 0 - sin θ cos θ 0 0001

R_{y} (θ) = cos θ 0 - sin θ 0 0100 sin θ 0 cos θ 0 0001

R_{z} (θ) = cos θ sin θ 00 - sin θ cos θ 00 00100001

任意旋转

任何3D旋转都可以由上面三个基本矩阵得到：

R_{x y z} (α, β, γ) = R_{x} (α) R_{y} (β) R_{z} (γ)

罗德里格旋转公式

绕旋转轴 $n = (n_{x}, n_{y}, n_{z})^{T}$ 旋转 $θ$ 的旋转矩阵：

R (n, θ) = cos θ I + (1 - cos θ) n n^{T} + sin θ 0 n_{z} - n_{y} - n_{z} 0 n_{x} n_{y} - n_{x} 0

MVP变换

引入

图形学中将3D空间的物体展现在2D屏幕上有十分重要的三个变换，以拍照片为例子，三个步骤是：

找到一个好场景，并安排好要拍照的人或物品（模型变换Model Transformation）

找到一个好角度放置相机（视图变换View Transformation）

按下快门，得到照片（投影变换Projection Transformation）

模型变换

3D物体有基于自身的坐标系表示，原点是只与这个物体有关的某个指定参考点。其他顶点的坐标值都是相对于这个原点而言的。

然后，将模型摆放到世界空间中指定的位置，需要依次进行缩放、旋转、平移操作，也就是：

M_{m o d e l} = T R S

p_{w or l d} = M_{m o d e l} p_{l oc a l}

变换前：模型空间(Local Space)
变换后：世界空间(World Space)

视图变换

确定一个相机需要三个向量：
相机位置 $e$ 、观测方向 $g$ （相机对着哪儿拍？）、向上方向 $t$ （横着，竖着，还是斜着拍？）

通常约定相机固定在原点，观测 $- z$ 方向，向上方向为 $y$ 。
现在试着将上面描述的相机移动到约定位置，我们需要以下步骤：

平移相机原本的中心点 $e$ 到原点；

旋转观测方向 $g$ 到 $- z$ ；

旋转向上方向 $t$ 到 $y$ ；

假设上述三个步骤可以用矩阵 $M_{v i e w}$ 表示，显然它们可以拆解为先平移、再旋转两步，也就是 $M_{v i e w} = R_{v i e w} T_{v i e w}$ ；
显然有：

T_{v i e w} = 100001000010 - x_{e} - y_{e} - z_{e} 1

接下来考虑旋转：我们想把 $g$ 方向旋转到 $- z$ ， $t$ 到 $y$ ，那么同时也会把 $g \times t$ 方向旋转到 $x$ 。然而这个变换并不好直接写出。因此我们现在考虑旋转操作的逆变换 $R_{v i e w}^{- 1}$ ：

$R_{v i e w}^{- 1}$ 的操作就是把 $x$ 方向旋转到 $g \times t$ ， $y$ 到 $t$ ， $z$ 到 $- g$ ：

R_{v i e w}^{- 1} = x_{g \times t} y_{g \times t} z_{g \times t} 0 x_{t} y_{t} z_{t} 0 x_{- g} y_{- g} z_{- g} 0 0001

旋转矩阵是正交阵，其转置等于逆，因此有：

R_{v i e w} = x_{g \times t} x_{t} x_{- g} 0 y_{g \times t} y_{t} y_{- g} 0 z_{g \times t} z_{t} z_{- g} 0 0001

p_{v i e w} = M_{v i e w} p_{w or l d}

变换前：世界空间(World Space)
变换后：观察空间(View Space)

投影变换

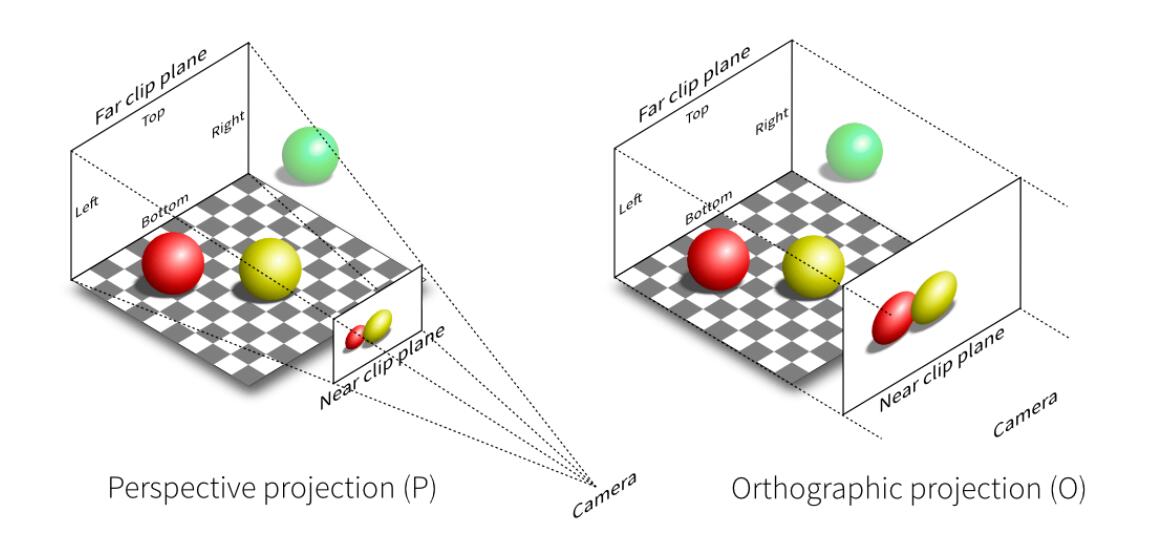
投影变换有如上图两种：正交投影(Orthographic Projection)和透视投影(Perspective Projection)。

正交投影

简单理解来说，正交投影的结果相当于直接丢弃了 $z$ 坐标，“拍扁”在 $x y$ 平面上。

正交投影更正式的做法是，我们希望将一个空间中 $[l, r] \times [b, t] \times [f, n]$ 的立方体变换至 $[- 1, 1]^{3}$ 。

这个过程可以分解为两步：先将立方体移动至中心与原点重合，再将各轴缩放至 $[- 1, 1]$ 范围。用矩阵表示为：

M_{or t h o} = 2/ (r - l) 000 0 2/ (t - b) 00 00 2/ (n - f) 0 0001 100001000010 - (l + r) /2 - (b + t) /2 - (f + n) /2 1 = \frac{2}{r - l} 000 0 \frac{2}{t - b} 00 00 \frac{2}{n - f} 0 \frac{l + r}{l - r} \frac{b + t}{b - t} \frac{f + n}{f - n} 1

透视投影

透视投影符合近大远小的视觉效果，观感上更为自然。透视投影可以首先将视锥体(View Frustum)“挤压”至长方体内，再应用正交投影：

M_{p er s p \to or t h o} = n 000 0 n 00 00 n + f 1 00 - n f 0

M_{p er s p} = M_{or t h o} M_{p er s p \to or t h o} = \frac{2 n}{r - l} 000 0 \frac{2 n}{t - b} 00 \frac{l + r}{l - r} \frac{b + t}{b - t} \frac{n + f}{n - f} 1 00 \frac{- 2 n f}{n - f} 0

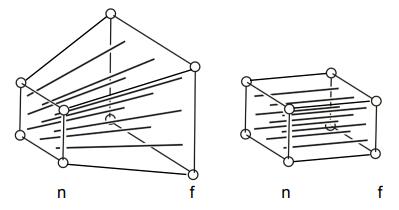
变换前：观察空间(View Space)
变换后：裁剪空间(Clip Space)

视口变换

视口变换希望在 $x y$ 平面上将 $[- 1, 1]^{2}$ 变换至屏幕上 $[0, w] \times [0, h]$ ，这个矩阵是：

M_{v i e w p or t} = w /2 000 0 h /2 00 0010 w /2 h /2 01

无论正交投影还是透视投影，物体在视锥体之外的部分将会变得不可见，这也是裁剪空间的得名。

变换前：裁剪空间(Clip Space)
变换后：屏幕空间(Screen Space)

Loading component...