本页目录

CSP 202012 T1-T5题解

T1 期末预测之安全指数

#include <iostream>
using namespace std;
int n,w,score,sum;
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>w>>score;
        sum+=w*score;
    }
    cout<<(sum<0?0:sum)<<endl;
    return 0;
}
/*
in:
6
2 60
10 100
0 70
0 0
-10 50
10 60

out:
1220
*/

T2 期末预测之最佳阈值

#include <iostream>
#include <algorithm>
using namespace std;
int n,y,res;
int best_score,best_theta,prev_theta;
int sum[100005];//第i大阈值(包含重复)res=1的总数
struct T{
    int y,res;
}t[100005];
bool cmp(T t1,T t2){return t1.y<t2.y;}
//第i大阈值(包含重复)预测正确次数
int getScore(int i)
{
    return (i-sum[i-1])+(sum[n-1]-sum[i-1]);
}
int main()
{
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>y>>res;
        t[i]=(T){y,res};
    }
    sort(t,t+n,cmp);
    sum[0]=t[0].res;
    for(int i=1;i<n;i++)
    {
        sum[i]=sum[i-1]+t[i].res;
    }
    best_theta=prev_theta=t[0].y;
    best_score=getScore(0);
    for(int i=1;i<n;i++)
    {
        if(t[i].y>prev_theta)
        {
            if(best_score<=getScore(i))
            {
                best_theta=t[i].y;
                best_score=getScore(i);
            }
            prev_theta=t[i].y;
        }
    }
    cout<<best_theta<<endl;
    return 0;
}
/*
in:
6
0 0
1 0
1 1
3 1
5 1
7 1

out:
3

in:
8
5 1
5 0
5 0
2 1
3 0
4 0
100000000 1
1 0

out:
100000000
*/

T3 带配额的文件系统

实在是麻烦。

#include <iostream>
#include <vector>
#include <map>
using namespace std;
int n;
char opt;
long long new_file_size,ld,lr;
string path;
struct NODE{
    bool isDir;
    string name;
    NODE *father;
    map<string,NODE*> childs;
    long long file_size,dir_size,child_size;
    long long ld,lr;
}root;
vector<string> split(string str,string sep)
{
    vector<string> res;
    int p=0;
    for(int i=str.find(sep);i!=-1;p=i+=sep.length(),i=str.find(sep,i))
        res.push_back(str.substr(p,i-p));
    res.push_back(str.substr(p,str.size()-p));
    return res;
}
//检查current路径中，如果文件大小增加了file_size_change，是否还满足配额
bool checkCreateOrUpdateFile(NODE *current,long long file_size_change)
{
    //检查自身的目录配额
    if(current->ld&&current->dir_size+file_size_change>current->ld)
    {
        return false;
    }
    //检查自身和祖先的后代配额
    for(NODE *p=current;p!=NULL;p=p->father)
    {
        if(p->lr&&p->child_size+file_size_change>p->lr)
        {
            return false;
        }
    }
    return true;
}
//更新祖先的已有配额
void updateLdAndLr(NODE *current,long long size_change)
{
    bool isDir=current->isDir;
    //更新祖先的已有后代配额
    for(NODE *p=current->father;p!=NULL;p=p->father)
    {
        p->child_size+=size_change;
    }
    //文件还会影响父亲的已有目录配额
    if(!isDir)
    {
        current->father->dir_size+=size_change;
    }
    return;
}
/*
创建普通文件

对于该指令，若路径所指的文件已经存在，且也是普通文件的，则替换这个文件；
若路径所指文件已经存在，但是是目录文件，则该指令不能执行成功。

当路径中的任何目录不存在时，应当尝试创建这些目录；
若要创建的目录文件与已有的同一双亲目录下的孩子文件中的普通文件名称重复，则该指令不能执行成功。

另外，还需要确定在该指令的执行是否会使该文件系统的配额变为不满足；
如果会发生这样的情况，则认为该指令不能执行成功，反之则认为该指令能执行成功。
*/
char C(string path,long long new_file_size)
{
    vector<string> dirs=split(path,"/");
    NODE *current=&root;
    int i;
    //检查目录节点
    for(i=1;i<dirs.size()-1;i++)
    {
        //发现同名
        if(current->childs[dirs[i]]!=NULL)
        {
            //存在同名目录
            if(current->childs[dirs[i]]->isDir)
            {
                current=current->childs[dirs[i]];//进入下一级
            }
            //存在同名文件
            else
            {
                return 'N';
            }
        }
        //不存在同名则考虑配额(决定要不要创建新目录)
        else
        {
            //配额检验
            //这一级一定是一个目录(这个for循环就是这样定义的)，因此不会对自身和任何祖先的已有目录配额产生影响
            //无论后面还有多少级别目录，都只有一个新文件，相当于使自身和所有祖先的已有后代配额增加文件大小
            for(NODE *p=current;p!=NULL;p=p->father)
            {
                if(p->lr&&p->child_size+new_file_size>p->lr)
                {
                    return 'N';
                }
            }
            //通过配额检验，可以创建新目录
            NODE *new_dir=new NODE();
            new_dir->isDir=true;
            new_dir->name=dirs[i];
            new_dir->father=current;
            new_dir->ld=0;
            new_dir->lr=0;
            new_dir->dir_size=0;
            new_dir->child_size=0;
            current->childs[dirs[i]]=new_dir;
            current=new_dir;
        }
    }
    //尝试创建文件但发现同名
    if(current->childs[dirs[i]]!=NULL)
    {
        //存在同名目录
        if(current->childs[dirs[i]]->isDir)
        {
            return 'N';
        }
        //存在同名文件
        else
        {
            long long old_file_size=current->childs[dirs[i]]->file_size;
            //配额检验
            if(!checkCreateOrUpdateFile(current,new_file_size-old_file_size))
            {
                return 'N';
            }
            current->childs[dirs[i]]->file_size=new_file_size;//仅替换
            //更新祖先的已有配额
            updateLdAndLr(current->childs[dirs[i]],new_file_size-old_file_size);
        }
    }
    //不存在同名则创建新文件
    else
    {
        //配额检验
        if(!checkCreateOrUpdateFile(current,new_file_size))
        {
            return 'N';
        }
        //通过配额检验，可以创建新文件
        NODE *new_file=new NODE();
        new_file->isDir=false;
        new_file->name=dirs[i];
        new_file->father=current;
        new_file->file_size=new_file_size;
        current->childs[dirs[i]]=new_file;
        //更新祖先的已有配额
        updateLdAndLr(new_file,new_file_size);
    }
    return 'Y';
}
/*
移除文件

若该路径所指的文件不存在，则不进行任何操作。

若该路径所指的文件是目录，则移除该目录及其所有后代文件。

在上述过程中被移除的目录（如果有）上设置的配额值也被移除。

该指令始终认为能执行成功。
*/
char R(string path)
{
    vector<string> dirs=split(path,"/");
    NODE *current=&root;
    int i;
    //检查节点
    for(i=1;i<dirs.size();i++)
    {
        //发现同名
        if(current->childs[dirs[i]]!=NULL)
        {
            current=current->childs[dirs[i]];//进入下一级
        }
        //不存在同名则不执行操作
        else
        {
            return 'Y';
        }
    }
    //更新祖先的已有配额
    updateLdAndLr(current,-(current->isDir?current->child_size:current->file_size));
    //断开与父亲的连接(注意：对于删除目录的情况可能产生内存垃圾)
    current->father->childs[dirs[i-1]]=NULL;
    current->father=NULL;
    return 'Y';
}
/*
设置配额值

该指令表示对所指的目录文件分别设置目录配额和后代配额。

若路径所指的文件不存在，或者不是目录文件，则该指令执行不成功。

若在该目录上已经设置了配额，则将原配额值替换为指定的配额值。

特别地，若配额值为0，则表示不对该项配额进行限制。

若在应用新的配额值后，该文件系统配额变为不满足，那么该指令执行不成功。
*/
char Q(string path,long long ld,long long lr)
{
    vector<string> dirs=split(path,"/");
    NODE *current=&root;
    int i;
    //检查节点
    for(i=0;i<dirs.size();i++)
    {
        if(dirs[i]=="") continue;//Q指令有可能输入根目录，此处特殊处理一下
        //发现同名
        if(current->childs[dirs[i]]!=NULL)
        {
            current=current->childs[dirs[i]];//进入下一级
        }
        //不存在同名则退出
        else
        {
            return 'N';
        }
    }
    if(!current->isDir) return 'N';
    if(ld&&current->dir_size>ld||lr&&current->child_size>lr) return 'N';
    current->ld=ld;
    current->lr=lr;
    return 'Y';
}
int main()
{
    root.isDir=true;
    root.name="root";
    cin>>n;
    for(int i=0;i<n;i++)
    {
        cin>>opt;
        if(opt=='C')
        {
            cin>>path>>new_file_size;
            cout<<C(path,new_file_size)<<endl;
        }
        else if(opt=='R')
        {
            cin>>path;
            cout<<R(path)<<endl;
        }
        else if(opt=='Q')
        {
            cin>>path>>ld>>lr;
            cout<<Q(path,ld,lr)<<endl;
        }
    }
    return 0;
}
/*
in:
10
C /A/B/1 1024
C /A/B/2 1024
C /A/B/1/3 1024
C /A 1024
R /A/B/1/3
Q / 0 1500
C /A/B/1 100
Q / 0 1500
R /A/B
Q / 0 1

out:
Y
Y
N
N
Y
N
Y
Y
Y
Y

in:
9
Q /A/B 1030 2060
C /A/B/1 1024
C /A/C/1 1024
Q /A/B 1024 0
Q /A/C 0 1024
C /A/B/3 1024
C /A/B/D/3 1024
C /A/C/4 1024
C /A/C/D/4 1024

out:
N
Y
Y
Y
Y
N
Y
N
N

in:
17
C /A/B/1 1024
C /A/B/2 1024
C /A/B/1/3 1024
C /A 1024
R /A/B/1/3
Q / 0 1500
C /A/B/1 100
Q / 0 1500
C /A/B/1 1024
R /A/B
Q / 0 1
C /A/B/1 1
Q /A/B/1 0 0
Q / 0 2500000000
C /A/B/2 1000000000
C /A/B/3 900000000
C /A/B/4 1000000000

out:
Y
Y
N
N
Y
N
Y
Y
N
Y
Y
Y
N
Y
Y
Y
N
*/

T4 食材运输

这题大概分成两步做：
第一步，树上DFS求对于特定的食材，选取特定的检查点，等待时间最长的酒店等待的最短时间；
第二步，二分求答案，check(x)函数为能否在m个检查点之内使得对于所有食材，等待时间最长的酒店等待的最短时间的最大值小于等于x。

第一步：树上DFS

每次DFS都是针对某种特定的食材j的，体现为代码中的int dfsReturn(int root,int j)、int dfsSingle(int root,int j)，但是下面为了便于描述，忽略这个食材种类j了。

树上DFS做两次：

第一次记录往返时间，也就是从当前酒店出发遍历子树所有的需要某种食材的酒店再回到当前酒店的时间；
下面公式中，记当前酒店含有需要这种食材的酒店的子树为 $i$ ， $w$ 是边权：

t_{re t u r n} (roo t) = \sum_{i} (t_{re t u r n} (i) + 2 w (roo t, i))

对于判断子树究竟含不含有需要这种食材的酒店，只需要看子树的 $t_{re t u r n}$ 非零，或者子树的根节点直接需要这种食材。

第二次记录单程时间，也就是从当前酒店出发遍历子树所有的需要某种食材的酒店，等待时间最长的酒店等待的最短时间。
考虑单程时间相比往返时间减少的部分，假如从当前节点 $roo t$ 选择的最后走一个子树分支 $i$ ，就不需要再从此路返回了。因此首先节省了一倍 $w (roo t, i)$ 的时间；其次，对于遍历这颗子树花费的时间，也从往返时间变成了单程时间，因此还可以节省 $t_{re t u r n} (i) - t_{s in g l e} (i)$ 的时间。因此有：

t_{s in g l e} (roo t) = t_{re t u r n} (roo t) - max_{i} {w (roo t, i) + t_{re t u r n} (i) - t_{s in g l e} (i)}

实现细节与第一步类似，具体见代码。

第二步：状压DP+二分

最小值最大或最大值最小的问题可以用二分求解，此题二分的check函数实质上是一个重复覆盖问题，可以用状压DP求解，具体见代码注释。

代码

#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
int n,m,k;
bool need[105][15];//need[i][j]：第i个酒店是否需要第j种食材
int tree[105][105];//n较小，用邻接矩阵存树
bool visit[105];
int t_return[105];//往返时间，t_return[i]：从i出发遍历子树所有需要某种食材的酒店再回到i的时间
int t_single[105];//单程时间，t_single[i]：从i出发遍历子树所有需要某种食材的酒店，等待时间最长的酒店等待的最短时间
int best[105][15];//best[i][j]：检查点设在第i个酒店时，运输第j种食材，等待时间最长的酒店等待的最短时间
int dfsReturn(int root,int j)
{
    visit[root]=1;
    for(int i=0;i<n;i++)
    {
        if(tree[root][i]&&!visit[i])
        {
            int ret=dfsReturn(i,j);
            if(ret||need[i][j])
            {
                t_return[root]+=2*tree[root][i]+ret;
            }
        }
    }
    return t_return[root];
}
int dfsSingle(int root,int j)
{
    visit[root]=1;
    int max_delta=0;
    for(int i=0;i<n;i++)
    {
        if(tree[root][i]&&!visit[i])
        {
            int sig=dfsSingle(i,j);
            if(sig||need[i][j])
            {
                max_delta=max(max_delta,tree[root][i]+t_return[i]-sig);
            }
        }
    }
    return t_single[root]=t_single[root]-max_delta;
}
//检查有没有可能在m行之内使得每列最小值的最大值<max_min_of_col
bool check(int max_min_of_col)
{
    int states[105]={};
    int dp[1<<10+5];
    memset(dp,0x3f,sizeof(dp));
    dp[0]=0;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<k;j++)
        {
            states[i]|=(best[i][j]<=max_min_of_col)<<j;
        }
    }
    for(int s=0;s<(1<<k);s++)
    {
        for(int i=0;i<n;i++)
        {
            dp[s|states[i]]=min(dp[s|states[i]],dp[s]+1);
        }
    }
    return dp[(1<<k)-1]<=m;
}
int main()
{
    cin>>n>>m>>k;
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<k;j++)
        {
            cin>>need[i][j];
        }
    }
    for(int i=0;i<n-1;i++)
    {
        int u,v,w;
        cin>>u>>v>>w;
        tree[u-1][v-1]=w;
        tree[v-1][u-1]=w;
    }
    //第一步，求出best[i][j]
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<k;j++)
        {
            //先求出针对第j种食材的往返时间t_return[i]
            memset(visit,0,sizeof(visit));
            memset(t_return,0,sizeof(t_return));
            dfsReturn(i,j);
            //然后求出针对第j种食材的单程时间
            memset(visit,0,sizeof(visit));
            for(int k=0;k<n;k++)
            {
                t_single[k]=t_return[k];
            }
            dfsSingle(i,j);
            //t_single[i]就是对于第j种食材，检查点设在第i个酒店时，等待时间最长的酒店等待的最短时间
            best[i][j]=t_single[i];
        }
    }
    //第二步，得到best[i][j]后，假设best[i][j]是
    //b11 b12 b13
    //b21 b22 b23
    //b31 b32 b33
    //b41 b42 b43
    //b51 b52 b53
    //这其中行代表酒店，列代表食材种类；
    //我们希望取出m行，求出m行对应的k列的最小值，再求这k个最小值中的最大值，然后让这个最大值最小
    //我们用二分去找这个最大值，check(x)定义为：如果最后的最大值不能超过x，是否能找到小于等于m的行数

    //考虑check(x)函数的实现，我们对best中每一项是否小于x建立一个01矩阵，假设结果为
    //0 0 1
    //0 0 0
    //0 1 1
    //0 1 0
    //1 0 1
    //那么check(x)就是在问，是否能找到不超过m行，使得m行相或为全1 (重复覆盖问题)
    //可以使用状态压缩dp求解

    //反向理解一下，如果能找到不超过m行，使得m行相或为全1，例如对于m=2找到了[0 1 1]和[1 0 1]
    //那么一定可以对于每一列j都选出一个值为1的行i，那么就可以使得第j种食材的检查点设在酒店i
    //值为1代表元素小于x，因为每列都至少有1个1，每列的最小值再求最大也一定小于x
    int l=0,r=1e9;
    while(l+1<r)
    {
        int mid=(l+r)>>1;
        if(!check(mid)) l=mid;
        else r=mid;
    }
    cout<<(check(l)?l:r)<<endl;
    return 0;
}
/*
in:
6 2 2
1 0
0 0
1 0
0 1
0 1
0 1
1 2 7
2 3 2
2 4 4
4 5 5
4 6 3

out:
9
*/

T5 星际旅行

运算符重载简化编码

线段树题，考虑到对三个坐标分开维护较为麻烦，考虑重载自定义POS类型的运算符，隐去三个坐标的内部逻辑，当作整体考虑：

struct POS{
    long long x,y,z;
    friend POS operator +(POS a,POS b)
    {
        POS ans;
        ans.x=(a.x+b.x)%MOD;
        ans.y=(a.y+b.y)%MOD;
        ans.z=(a.z+b.z)%MOD;
        return ans;
    }
    friend POS operator *(POS a,long long k)
    {
        POS ans;
        ans.x=(a.x*k)%MOD;
        ans.y=(a.y*k)%MOD;
        ans.z=(a.z*k)%MOD;
        return ans;
    }
    friend POS operator <<(POS a,int k)
    {
        k=k%3;
        if(k==0) return a;
        else if(k==1)
        {
            POS ans;
            ans.x=a.y;
            ans.y=a.z;
            ans.z=a.x;
            return ans;
        }
        else if(k==2)
        {
            POS ans;
            ans.x=a.z;
            ans.y=a.x;
            ans.z=a.y;
            return ans;
        }
    }
};

对于要维护的转向操作，实际上逻辑类似对(x,y,z)进行循环左移，这里就重载左移运算符来表示。根据题意，每次操作只会左移至多1位。

线段树懒标记优先级

线段树题中有一种类就是会有多个懒标记，需要我们指定优先级，例如经典的“先乘后加”洛谷P3373【模板】线段树2。此题涉及了三种运算：乘、加、左移，需要保证先乘后加，左移的优先级任意。这里以左移优先级最后为例分析懒标记的合并。

个人理解

事实上懒标记的优先级不存在严格正确的答案，只要可以推出合并公式，就是正确的方案。至于前面提到的为什么要“先乘后加”而不能“先加后乘”，这是因为如果指定优先级为“先加后乘”，最后的合并公式中会出现分数。这在数学上其实是完全可行的，只是不方便编程实现，所以结论是一定要先做乘法。

考虑自己当前的标记是(mul a,add b,lshift c)，注意这里a、c是常数，b是一个三维向量(b1,b2,b3)。这个标记作用于p=(x,y,z)，可以得到：

先乘：p=(ax,ay,az)

再加：p=(ax+b1,ay+b2,az+b3)

最后左移（暂且假设c=1）：p=(ay+b2,az+b3,ax+b1)

接下来考虑父亲pushdown给自己另外一个标记(mul g,add h,lshift i)，继续作用于p可以得到：

先乘：p=(g(ay+b2),g(az+b3),g(ax+b1))

再加：p=(g(ay+b2)+h1,g(az+b3)+h2,g(ax+b1)+h3)

最后左移（暂且假设i=1）：p=(g(az+b3)+h2,g(ax+b1)+h3,g(ay+b2)+h1)

合并公式就是在考虑，如何只用一个懒标记（也就是合并后的懒标记）去表示这两个懒标记的复合操作。

观察乘法标记，显然合并后的乘法标记是mul ag；

观察加法标记，注意b1是与x绑定的，加法项中一定有一项bg；再看h是发生了错位的，现在仔细考虑这个问题：
h发生错位是因为操作lshift c，还是操作lshift i？
答案是lshift c。根据我们指定的优先级，左移操作在最后，在add h时显然还没有lshift i。

因为在add h之前p就发生了lshift c，那么相对地，此时在进行add h，相当于在没有位移时进行add (h>>c)。当然，我们没定义右移，但可以用左移等价表示为add (h<<(3-c))。
因此合并后的加法标记是add bg+(h<<(3-c))；

观察左移标记，显然合并后的左移标记是lshift (c+i)%3；

这就是最终的合并公式：(mul ag,add bg+(h<<(3-c)),lshift (c+i)%3)。

如果不想看推导过程，只需要从p=(x,y,z)出发，验证只经过一次上述操作（先乘ag，再加bg+(h<<(3-c))，再左移(c+i)%3），即可得到p=(g(az+b3)+h2,g(ax+b1)+h3,g(ay+b2)+h1)。

对应在代码中就是：

//合并tgv至 <管辖[l,r]区间的f节点> 的tag值，同时更新树上值
void mergetag(int l,int r,int f,TAGVAL tgv)
{
    //原本TAG(*a,+b,<<c)，父亲分发下TAG(*g,+h,<<i)
    //现在TAG(*ag,+bg+(h<<(3-c)),<<(c+i))
    long long a=tree[f].tag.mul,g=tgv.mul;
    POS b=tree[f].tag.add,h=tgv.add;
    int c=tree[f].tag.rot,i=tgv.rot;

    //更新树上值
    int len=r2q[r]-r2q[l-(l&1^1)]+(l&1);
    tree[f].p=(tree[f].p*g+h*len)<<i;

    //更新懒标记
    tree[f].tag.mul=(a*g)%MOD;
    tree[f].tag.add=b*g+(h<<(3-c));
    tree[f].tag.rot=(c+i)%3;
    tree[f].flag=true;
    return;
}

离散化

题目给的数据范围需要离散化，这里我的方案是：

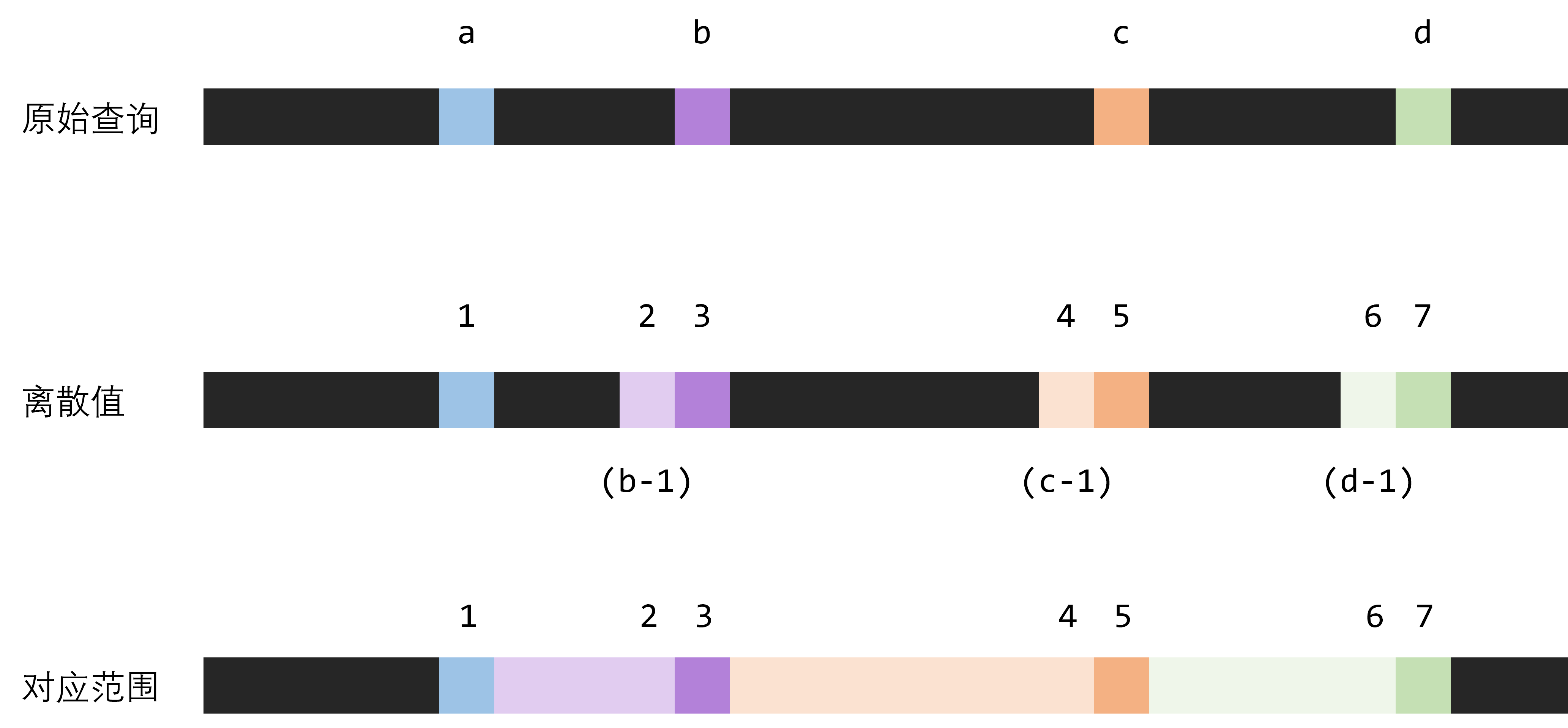
考虑维护区间和时，我们需要得到区间长度。在不离散化时，长度就是r-l+1。现在我们记f(x)就是离散化值x对应的原始值，在代码中对应r2q[x]。在图中，f(1)=a、f(2)=b-1、f(3)=b、f(4)=c-1、f(5)=c……

查询离散区间(x,y)对应的原始区间长度，右侧一定是f(y)，左侧根据x的奇偶性，有：

len=f(y)-f(x)+1，x是奇数

len=f(y)-f(x-1)，x是偶数

也就是代码中的：

int len=r2q[r]-r2q[l-!(l&1)]+(l&1);

代码

#include <iostream>
#include <vector>
#include <map>
#include <set>
#define N 160005
#define MOD 1000000007
using namespace std;
int n,m;
int opt[40005][6];//记录操作
vector<int> raw;//原始的查询
vector<int> r2q;//rank to query，r2q[i]是rank为i的查询
map<int,int> q2r;//query to rank，q2r[q]是查询q对应的rank
int lc(int f){return f<<1;}//左子
int rc(int f){return f<<1|1;}//右子

struct POS{
    long long x,y,z;
    friend POS operator +(POS a,POS b)
    {
        POS ans;
        ans.x=(a.x+b.x)%MOD;
        ans.y=(a.y+b.y)%MOD;
        ans.z=(a.z+b.z)%MOD;
        return ans;
    }
    friend POS operator *(POS a,long long k)
    {
        POS ans;
        ans.x=(a.x*k)%MOD;
        ans.y=(a.y*k)%MOD;
        ans.z=(a.z*k)%MOD;
        return ans;
    }
    friend POS operator <<(POS a,int k)
    {
        k=k%3;
        if(k==0) return a;
        else if(k==1)
        {
            POS ans;
            ans.x=a.y;
            ans.y=a.z;
            ans.z=a.x;
            return ans;
        }
        else if(k==2)
        {
            POS ans;
            ans.x=a.z;
            ans.y=a.x;
            ans.z=a.y;
            return ans;
        }
    }
};

struct TAGVAL{
    long long mul;
    POS add;
    int rot;
}const DEFAULT_TAG{1,POS{0,0,0},0};

struct NODE{
    POS p;
    bool flag;//是否打了tag
    TAGVAL tag;
}tree[4*N];

//合并tgv至 <管辖[l,r]区间的f节点> 的tag值，同时更新树上值
void mergetag(int l,int r,int f,TAGVAL tgv)
{
    //原本TAG(*a,+b,<<c)，父亲分发下TAG(*g,+h,<<i)
    //现在TAG(*ag,+bg+(h<<(3-c)),<<(c+i))
    long long a=tree[f].tag.mul,g=tgv.mul;
    POS b=tree[f].tag.add,h=tgv.add;
    int c=tree[f].tag.rot,i=tgv.rot;

    int len=r2q[r]-r2q[l-!(l&1)]+(l&1);
    tree[f].p=(tree[f].p*g+h*len)<<i;
    tree[f].tag.mul=(a*g)%MOD;
    tree[f].tag.add=b*g+(h<<(3-c));
    tree[f].tag.rot=(c+i)%3;
    tree[f].flag=true;
    return;
}

//用子节点更新 <f节点>
void pushup(int f)
{
    tree[f].p=tree[lc(f)].p+tree[rc(f)].p;
    return;
}

//将 <管辖[l,r]区间的f节点> 的tag值下发至子节点
void pushdown(int l,int r,int f)
{
    if(l==r) return;
    int mid=l+(r-l)/2;
    mergetag(l,mid,lc(f),tree[f].tag);
    mergetag(mid+1,r,rc(f),tree[f].tag);
    tree[f].tag=DEFAULT_TAG;
    tree[f].flag=false;
    return;
}

//在tree[f]建立一个管辖[l,r]的节点
void build(int l,int r,int f)
{
    tree[f].flag=false;
    tree[f].tag=DEFAULT_TAG;
    if(l==r)
    {
        tree[f].p=POS{0,0,0};
        return;
    }
    int mid=l+(r-l)/2;
    build(l,mid,lc(f));
    build(mid+1,r,rc(f));
    pushup(f);
    return;
}

//将tgv合并至区间[ql,qr]的tag值，当前在管辖[l,r]区间的f节点
void update(int ql,int qr,int l,int r,int f,TAGVAL tgv)
{
    //当前区间是查询区间的子集，修改
    if(ql<=l&&r<=qr)
    {
        mergetag(l,r,f,tgv);
        return;
    }
    int mid=l+(r-l)/2;
    if(tree[f].flag) pushdown(l,r,f);//访问到有标记的节点就下放
    if(ql<=mid) update(ql,qr,l,mid,lc(f),tgv);
    if(qr>mid) update(ql,qr,mid+1,r,rc(f),tgv);
    pushup(f);
    return;
}

//求区间[ql,qr]的和，当前在管辖[l,r]区间的f节点
POS getsum(int ql,int qr,int l,int r,int f)
{
    //当前区间是查询区间的子集，返回
    if(ql<=l&&r<=qr) return tree[f].p;
    int mid=l+(r-l)/2;
    if(tree[f].flag) pushdown(l,r,f);//访问到有标记的节点就下放
    POS ans={0,0,0};
    if(ql<=mid) ans=ans+getsum(ql,qr,l,mid,lc(f));
    if(qr>mid) ans=ans+getsum(ql,qr,mid+1,r,rc(f));
    return ans;
}

int main()
{
    ios::sync_with_stdio(false);
    cin>>n>>m;
    for(int i=0;i<m;i++)
    {
        int q;
        cin>>q;
        opt[i][0]=q;
        if(q==1)
        {
            cin>>opt[i][1]>>opt[i][2]>>opt[i][3]>>opt[i][4]>>opt[i][5];
        }
        else if(q==2)
        {
            cin>>opt[i][1]>>opt[i][2]>>opt[i][3];
        }
        else if(q==3)
        {
            cin>>opt[i][1]>>opt[i][2];
        }
        else
        {
            cin>>opt[i][1]>>opt[i][2];
        }
        raw.emplace_back(opt[i][1]);
        raw.emplace_back(opt[i][2]);
    }

    //离散化
    set<int> tmp(raw.begin(),raw.end());
    raw.assign(tmp.begin(),tmp.end());//对raw去重+排序
    for(int i=0;i<raw.size();i++)
    {
        r2q.emplace_back(raw[i]-1);
        r2q.emplace_back(raw[i]);
    }
    n=r2q.size()-1;//不计算0
    for(int i=1;i<=n;i+=2) q2r[r2q[i]]=i;//通过真实查询值反查rank

    build(1,n,1);
    for(int i=0;i<m;i++)
    {
        int q,l,r,a,b,c,k;
        q=opt[i][0];
        l=q2r[opt[i][1]];
        r=q2r[opt[i][2]];
        if(q==1)
        {
            a=opt[i][3];
            b=opt[i][4];
            c=opt[i][5];
            update(l,r,1,n,1,TAGVAL{1,POS{a,b,c},0});
        }
        else if(q==2)
        {
            k=opt[i][3];
            update(l,r,1,n,1,TAGVAL{k,POS{0,0,0},0});
        }
        else if(q==3)
        {
            update(l,r,1,n,1,TAGVAL{1,POS{0,0,0},1});
        }
        else
        {
            POS p=getsum(l,r,1,n,1);
            long long ans=p.x*p.x+p.y*p.y+p.z*p.z;
            cout<<ans%MOD<<'\n';
        }
    }
    return 0;
}
/*
in:
5 5
1 2 4 5 6 7
3 5 5
2 1 2 4
4 1 3
4 2 5

out:
2750
3960
*/