本页目录
CSP 202006 T1-T4题解
T1 线性分类器
#include <iostream>
using namespace std;
int n,m;
int p[1005][3];
int label[1005];//每个点根据直线的分类
bool check(int t0,int t1,int t2)
{
int sum=0;
for(int i=0;i<n;i++)
{
label[i]=t0+t1*p[i][0]+t2*p[i][1]>0;
//希望label[i]与p[i][3]全相等或全相反
sum+=label[i]^p[i][2];
}
return sum==0||sum==n;
}
int main()
{
cin>>n>>m;
for(int i=0;i<n;i++)
{
int x,y;
char ch;
cin>>x>>y>>ch;
p[i][0]=x;
p[i][1]=y;
p[i][2]=ch=='A';
}
for(int i=0;i<m;i++)
{
int t0,t1,t2;
cin>>t0>>t1>>t2;
cout<<(check(t0,t1,t2)?"Yes":"No")<<endl;
}
return 0;
}
/*
in:
9 3
1 1 A
1 0 A
1 -1 A
2 2 B
2 3 B
0 1 A
3 1 B
1 3 B
2 0 A
0 2 -3
-3 0 2
-3 1 1
out:
No
No
Yes
*/
T2 稀疏向量
#include <iostream>
#include <map>
using namespace std;
int n,a,b;
int idx,val;
long long ans;
map<int,int> ma,mb;
int main()
{
cin>>n>>a>>b;
for(int i=0;i<a;i++)
{
cin>>idx>>val;
ma[idx]=val;
}
for(int i=0;i<b;i++)
{
cin>>idx>>val;
mb[idx]=val;
}
auto ia=ma.begin(),ib=mb.begin();
for(;ia!=ma.end()&&ib!=mb.end();)
{
int idxa=ia->first,idxb=ib->first;
if(idxa>idxb)
{
ib++;
}
else if(idxa<idxb)
{
ia++;
}
else
{
ans+=ma[idxa]*mb[idxb];
ia++,ib++;
}
}
cout<<ans<<endl;
return 0;
}
/*
in:
10 3 4
4 5
7 -3
10 1
1 10
4 20
5 30
7 40
out:
-20
*/
T3 Markdown渲染器
本题输入量大,建议做一下读入优化:
ios::sync_with_stdio(false);
std::cin.tie(0);
另外,下面的源代码包含了输出渲染内容的功能(为了方便调试),修改变量bool dbg=1;即可。这样会输出:
10
01|CSP
02|
03|CSP.is.a.r
04|eal.realre
05|alrealreal
06|real.compe
07|tition.
08|
09|Come...and
10|join...us
解题代码为:
#include <iostream>
#include <vector>
using namespace std;
int w;
string s;
int cursor;//光标位置,cursor<=w
int line;//光标所在行
int rendering=0;//0:等待新内容 1:正在渲染段落 2:正在渲染列表
//字符串工具
string replace(string str,string str1,string str2)
{
string res=str;
for(int i=str.find(str1);i!=-1;i=str.find(str1,i+str1.size()))
res.replace(i,str1.size(),str2);
return res;
}
bool isEmpty(string str)
{
for(auto ch:str)
{
if(ch!=' ') return false;
}
return true;
}
/***************************************************************/
//调试
bool dbg=1;//输出最终渲染的结果
bool dbg_show_enterer=0;//输出是谁调用了换行
vector<string> dbg_result;
void dbg_show_result()
{
int line_id=1;//行号只补全一位,总行数最好不要超过100
for(auto str:dbg_result)
{
cout<<(line_id<10?"0":"")<<line_id<<"|"<<replace(str," ",".")<<endl;
line_id++;
}
return;
}
/***************************************************************/
void enter(string enterer="")
{
line++;
cursor=0;
if(dbg)
{
if(dbg_show_enterer) dbg_result.push_back(enterer);
else dbg_result.push_back("");
}
return;
}
void render(string s,bool padding=false)
{
while(s.back()==' ') s.pop_back();
int sz=s.size();
int str_p=0;//字符串指针,str_p<str.size()
//输入只有*_
if(sz==0&&padding)
{
if(dbg)
{
dbg_result.back()+="---";
}
cursor=3;
}
while(str_p<sz)
{
while(str_p<sz&&s[str_p]==' ') str_p++;
//连续输入两行之间插入一个空格
if(0<cursor&&cursor<w)
{
if(dbg)
{
dbg_result.back()+=" ";
}
cursor++;
}
if(cursor==w) enter("R:");
if(padding&&cursor==0)
{
if(dbg)
{
dbg_result.back()+="---";
}
cursor=3;
}
//剩余字符串还够渲染完当前行
if(w-cursor<=sz-str_p)
{
if(dbg)
{
dbg_result.back()+=s.substr(str_p,w-cursor);
}
str_p+=w-cursor;
cursor=w;
}
else
{
if(dbg)
{
dbg_result.back()+=s.substr(str_p);
}
cursor+=sz-str_p;
break;
}
}
return;
}
int main()
{
ios::sync_with_stdio(false);
std::cin.tie(0);
cin>>w;
getline(cin,s);
while(getline(cin,s))
{
if(isEmpty(s))
{
if(cursor) enter("A:");
rendering=0;
}
else
{
if(cursor==0) enter("B:");
//*_开头的行
if(s.size()>=2&&s[0]=='*'&&s[1]==' ')
{
if(rendering==0);
else if(rendering==1)
{
enter("C:");
enter("C:");
}
else if(rendering==2) enter("D:");
rendering=2;
render(s.substr(2),true);
}
//__开头的行
else if(s.size()>=2&&s[0]==' '&&s[1]==' ')
{
if(rendering==0) rendering=1,render(s);
else if(rendering==1) render(s);
else if(rendering==2) render(s.substr(2),true);
}
//普通的非空行
else
{
if(rendering==0);
else if(rendering==1);
else if(rendering==2)
{
enter("E:");
enter("E:");
}
rendering=1;
render(s);
}
}
}
if(cursor==0) line--;
cout<<line<<endl;
if(dbg)
{
dbg_show_result();
}
return 0;
}
/*
in:
10
CSP
CSP is
a real realrealrealrealreal
competition.
Come and join us
out:
10
in:
10
* CSP
* CSP is
* a real
competition.
*
* Come! and join.
*Tel:
* 12345
*
out:
14
*/
T4 1246
将状态转移化为矩阵快速幂
首先本题的核心都是围绕这个矩阵展开的:
//dt=1,四个数字的生成能力
vector<int> G={
0,1,0,0,
0,0,1,0,
1,0,0,1,
0,0,1,1,
};
这个矩阵代表1、2、4、6四个数字在t=1时间内能生成多少其他数字。在t=2时间内的生成能力就是,以此类推有:
对于一个初始状态,时间t之后的四个数字的数量是。
对于这道题,,它和相乘实际上得到的是的第一行。这也是题目中查询字符串长度为1时的解。对于的求解,由于,需要使用快速幂求解。
两位状态转移
查询字符串长度为2时,它们之间的生成关系是:
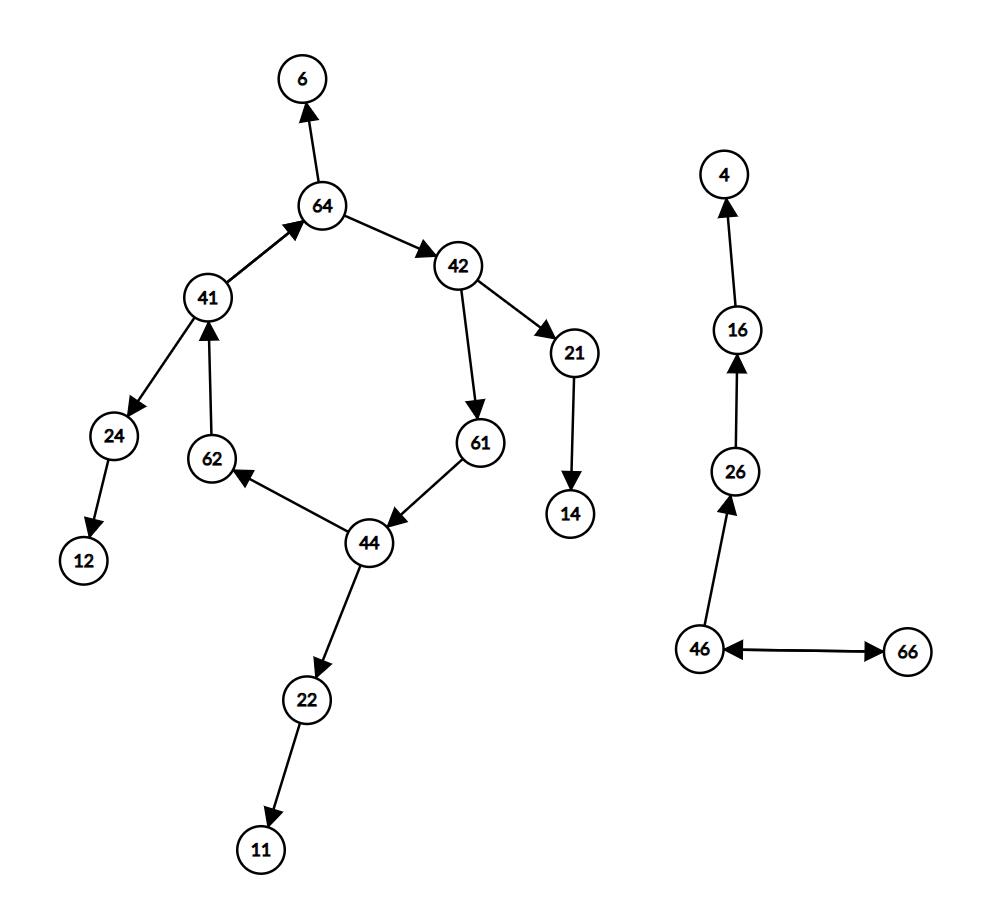
这里的箭头是一种“被生成”关系,例如62可以被41生成,例如41可以被64生成,64可以被6生成。
这个图中描述的生成关系是一定由两位都参与了的,举个例子,42的下一状态是164,但我们并不认为16可以被42生成,因为事实上2并没有参与这个过程(好好理解一下)。
从图中还可以看出,一定不会有12、24、22、11、21、14这六个组合出现,因为它们无法被4或6生成。
注意图中有两个环,在被6生成的数中有一个长度为6的环,在被4生成的数中有一个长度为2的环。
矩阵等比数列求和
这一步应该是我和绝大部分题解做的不一样的地方,大多数题解都是将1位或2位的状态合在一个大矩阵里考虑的。我自己做的时候就想都往最初的矩阵上靠,所以后面扯到了一些比较难搞的数学操作。
现在这样考虑,举个例子,看上面的状态图,我们知道一个6在t=2时间就会生成一个41,不过由于有环的存在,在t=8、t=14等等也会生成一个41。所以反过来想,如果想知道t时刻生成的41的数量,就等于:t-2时刻的4的数量t-8时刻的4的数量t-14时刻的4的数量...
也就是需要求:。
这其中有两个参数,第一个是第一项的指数,这取决于查询的两位数在图中最少需要经过几步被4或6生成;第二个是等比数列的公比,如果生成数是6,则循环周期为6,公比为;如果生成数是4并且查询的是46或66,则循环周期为2,公比为。
对矩阵进行等比数列求和和普通数列一样,只不过最后的除法要转换为乘以矩阵的逆;又因为公比只有两种,所以只需要提前计算和。
vector<int> _9xinv2={-6,-3,-3,6,-3,-6,3,3,3,-3,-3,6,3,6,6,-3};//9*inv(G^2-I)
vector<int> _9xinv6={-7,-5,4,1,4,-7,-4,5,-4,4,-2,1,5,1,1,-2}; //9*inv(G^6-I)
在代码中储存的是9倍逆矩阵的值,以保证元素是整数;在后续的计算中需要除以9,但又由于涉及到取模,需要改为乘以9对于998244353的逆元443664157。
到这一步,我们已经可以求出对于查询字符串长度为1或2时的解。
查询长度大于2的字符串
首先,3位及以上的状态不会出现环,这是因为,我们的定义要求所有位都参与生成,对于一个三位的状态xyz去生成下一个状态abc,最极端的情况是x左侧结合一位生成a, z右侧结合一位生成c,但y只能直接生成b。这样中间位一定会在一或两步之后变成1,然后不再能生成新的三位状态。
查询长度大于2的字符串,我们通过DFS寻找其2位的生成串,找到一个就按照前面的方法增加答案。
代码
#include <iostream>
#include <vector>
#define N 4
#define MOD 998244353
using namespace std;
int n,ans;
string s;
//0-15整数转2位字符串
string i2s(int x)
{
char chs[]={'1','2','4','6'};
return string(1,chs[x/4])+string(1,chs[x%4]);
}
//1位字符串转为0-3,2位字符串转为0-15
int s2i(string s)
{
int idx[]={0,0,1,0,2,0,3};
if(s.size()==1) return idx[s[0]-'0'];
return idx[s[0]-'0']*4+idx[s[1]-'0'];
}
//dt=1,四个数字的生成能力
vector<int> G={
0,1,0,0,
0,0,1,0,
1,0,0,1,
0,0,1,1,
};
//矩阵减法
vector<int> matsub(vector<int> A,vector<int> B)
{
vector<int> ans(N*N);
for(int i=0;i<N*N;i++) ans[i]=A[i]-B[i];
return ans;
}
//矩阵乘法,如果结果需要除以常数,则传入常数的逆元
vector<int> matmul(vector<int> A,vector<int> B,int inv_c=1)
{
vector<int> ans(N*N);
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
{
long long ansij=0;
for(int k=0;k<N;k++)
{
ansij+=((long long)A[i*N+k]*B[k*N+j])%MOD;
}
ansij=(ansij*inv_c)%MOD;//除以常数
ans[i*N+j]=(ansij+MOD)%MOD;
}
}
return ans;
}
//矩阵快速幂A^n
vector<int> fmp(vector<int> A,int n)
{
vector<int> ans(N*N);
for(int i=0;i<N;i++) ans[i*N+i]=1;
while(n)
{
if(n%2) ans=matmul(ans,A);
A=matmul(A,A);
n>>=1;
}
return ans;
}
//矩阵等比数列求和 A^t_start+A^(t_start-cyc)+A^(t_start-2*cyc)... (直到指数非正)
//生成数是4则循环周期cyc=2,生成数是6则循环周期cyc=6
vector<int> seqsum(vector<int> A,int t_start,int cyc)
{
int t_end=t_start-(t_start/cyc)*cyc;
vector<int> _9xinv2={-6,-3,-3,6,-3,-6,3,3,3,-3,-3,6,3,6,6,-3};//9*inv(G^2-I)
vector<int> _9xinv6={-7,-5,4,1,4,-7,-4,5,-4,4,-2,1,5,1,1,-2}; //9*inv(G^6-I)
//逆矩阵还需要除以9,因此传入9对于MOD(998244353)的逆元443664157
if(cyc==2) return matmul(_9xinv2,matsub(fmp(A,t_start+cyc),fmp(A,t_end)),443664157);
return matmul(_9xinv6,matsub(fmp(A,t_start+cyc),fmp(A,t_end)),443664157);
}
//判断是否为"整串",即可以从左侧开始恰好找到对应的"生成串"
bool isExact(string str)
{
for(int i=0;i<str.size();i++)
{
if(str[i]=='1')
{
if(str[++i]!='6') return false;
}
else if(str[i]=='6')
{
if(str[++i]!='4') return false;
}
}
return true;
}
//返回"整串"的"生成串"
string getGenerator(string str)
{
string ans;
for(int i=0;i<str.size();i++)
{
if(str[i]=='1') i++,ans+="4";
else if(str[i]=='6') i++,ans+="6";
else if(str[i]=='2') ans+="1";
else if(str[i]=='4') ans+="2";
}
return ans;
}
//返回2位字符串str在t=t0时出现的次数
int getAns(string str,int t0)
{
int t4[16]={0,0,0,1,0,0,0,2,0,0,0,3,0,0,0,4};
int t6[16]={0,0,0,0,0,0,0,0,2,6,4,0,5,3,1,0};
if(str.back()=='6')
{
int t=t4[s2i(str)];
if(str=="16"||str=="26") return fmp(G,t0-t)[2];
else return seqsum(G,t0-t,2)[2];
}
else
{
int t=t6[s2i(str)];
return t?seqsum(G,t0-t,6)[3]:0;
}
}
//对于长度大于等于3的字符串,dfs寻找其2位生成串
void dfs(string str,int t)
{
if(str.size()==2) {
ans=(ans+getAns(str,n-t))%MOD;
return;
}
vector<string> candidate={str};
if(str[0]=='4') candidate.push_back("6"+str);
else if(str[0]=='6') candidate.push_back("1"+str);
int len=candidate.size();
for(int i=0;i<len;i++)
{
string c=candidate[i];
if(c.back()=='1') candidate.push_back(c+"6");
else if(c.back()=='6')
{
if(!isExact(c)) candidate.push_back(c+"4");
}
}
for(auto c:candidate)
{
if(isExact(c)) dfs(getGenerator(c),t+1);
}
return;
}
int main()
{
cin>>n>>s;
if(s.size()==1)
{
ans=fmp(G,n)[s2i(s)];
}
else if(s.size()==2)
{
ans=getAns(s,n);
}
else
{
dfs(s,0);
}
cout<<ans<<endl;
return 0;
}
/*
in:
9
26
out:
5
in:
2020
16
out:
292008622
*/