本页目录
【模式识别】非参数估计
本章讨论的是非参数估计。很多时候我们无法给出样本分布的函数形式,也就无法使用根据样本估计函数参数的思路。
非参数估计的思想是,直接根据样本,用数值方法估计出整个分布函数。
非参数估计的基本原理
还记得用频率估计概率的经典思想吗!假设你掷了1000次硬币,发现有489次正面朝上,那么你估计掷这枚硬币正面朝上的概率是0.489,或者近似地,概率约为0.5。
现在我们来考虑更复杂一点的情况,要估计的不是某个概率数值,而是样本分布的概率密度函数。考虑概率密度的性质:概率密度函数在区间下的面积即为样本落在区间内的概率。
表述的更抽象一点,我们要估样本出现在面积为的一个小区域中的概率,这里的就相当于上面例子中的区间,。
总样本数为,落到小区域内的样本数为时,如果区域面积合适地小,我们就可以认为在区域内的概率密度是一个常数:
直方图方法
直方图方法非常简单,可以理解为近似的用直方图的形状取描述概率密度函数。
不过,在样本数量并非无限时,如果小舱(直方图组距)过大,那么最终估计出的密度函数就非常粗糙;如果过小,那么有的小舱内可能没有样本,估计出的概率密度函数很不连续。
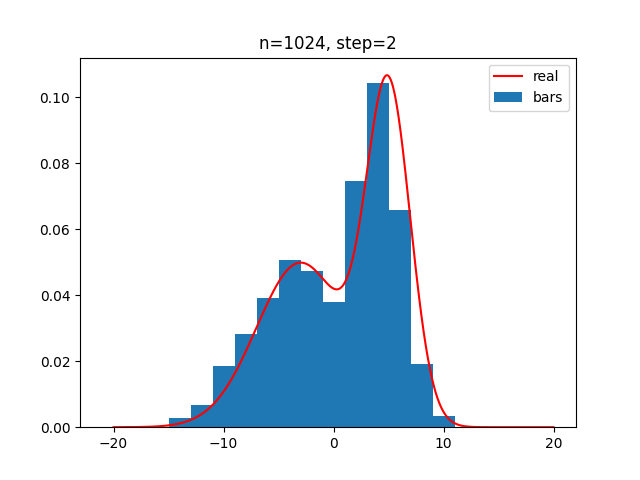
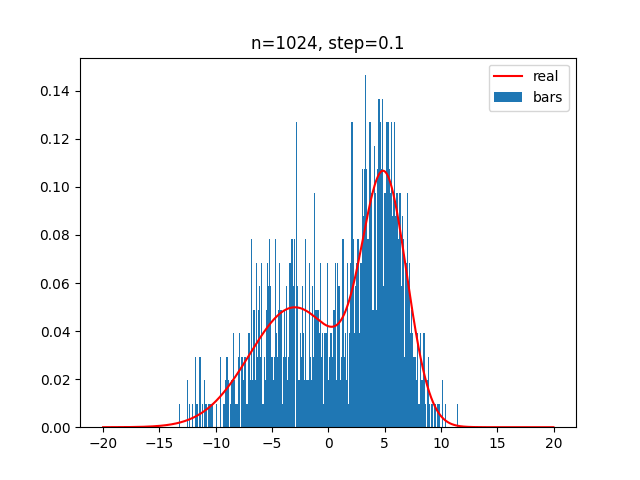
小舱的选择应该与样本总数相适应。如果样本总数是,小舱体积是,在附近落入小舱的样本个数是,那么估计的概率密度可以收敛于真实概率密度的条件是:
可以这样理解:小舱体积应该尽可能小,同时要保证小舱内有充分多的样本,但每个小舱内样本数又必须是总样本数中很小一部分。
k近邻估计
kNN的全称是k Nearest Neighbors,意思是K个最近的邻居。基本做法是:根据样本总数确定一个参数,例如样本总数为时,可以取
在求处的密度估计时,通过调整包含的小舱体积,直到小舱内恰好落入个样本。此时有:
使用kNN方法时,样本密度较高的地方小舱体积会比较小,而样本密度低的地方小舱体积自动增大。这样可以兼顾高密度区域的分辨率和低密度区域的连续性。
Parzen窗法
在这种方法中,我们会定义一个核函数(也称窗函数),其含义是,一个观测样本对在处概率密度估计的贡献。概率密度估计就是在每一点上把所有观测样本的贡献进行平均,即:
窗函数只需要本身满足概率密度函数的要求即可:
且
下面列举几种常见的窗函数。上文中样本都简单地用表示,下面仍然回到最一般的情况:
假设样本有个维度,记样本为。
方窗
方窗范围可以看作以为中心的超立方体,其代表窗口大小的参数是立方体棱长。
高斯窗(正态窗)
高斯窗范围即以样本为均值,协方差矩阵为的正态分布。
一维情况下有:
超球窗
超球窗范围可以看作以为中心的超球体,体积为,半径为。
这些窗函数中都有一个表示窗口宽度的参数(//),也称作平滑参数,它反映了一个样本可以对多大范围内的密度估计产生影响。
下面是在样本数和平滑参数不同时,使用方窗和高斯窗的估计结果:
方窗
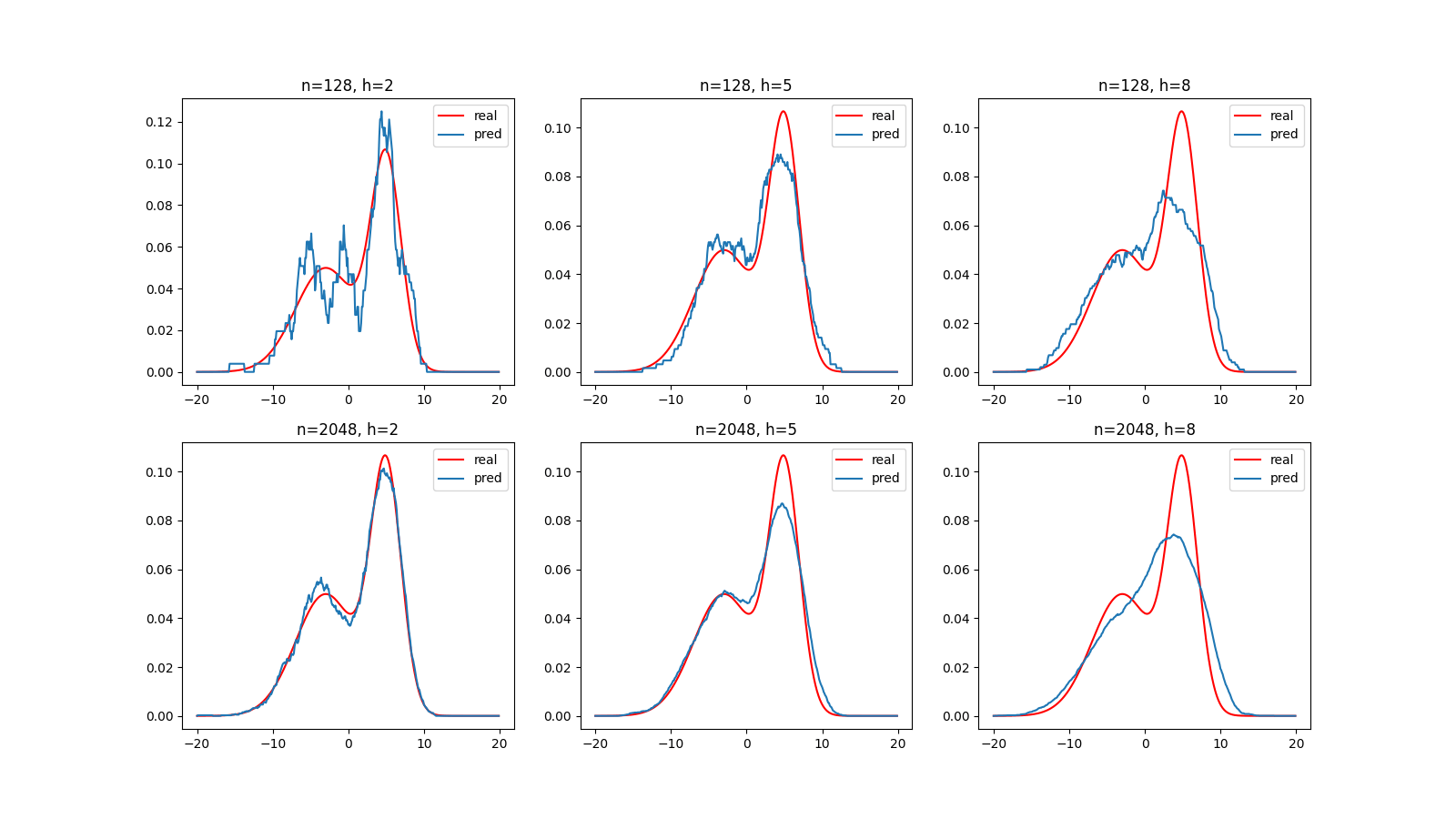
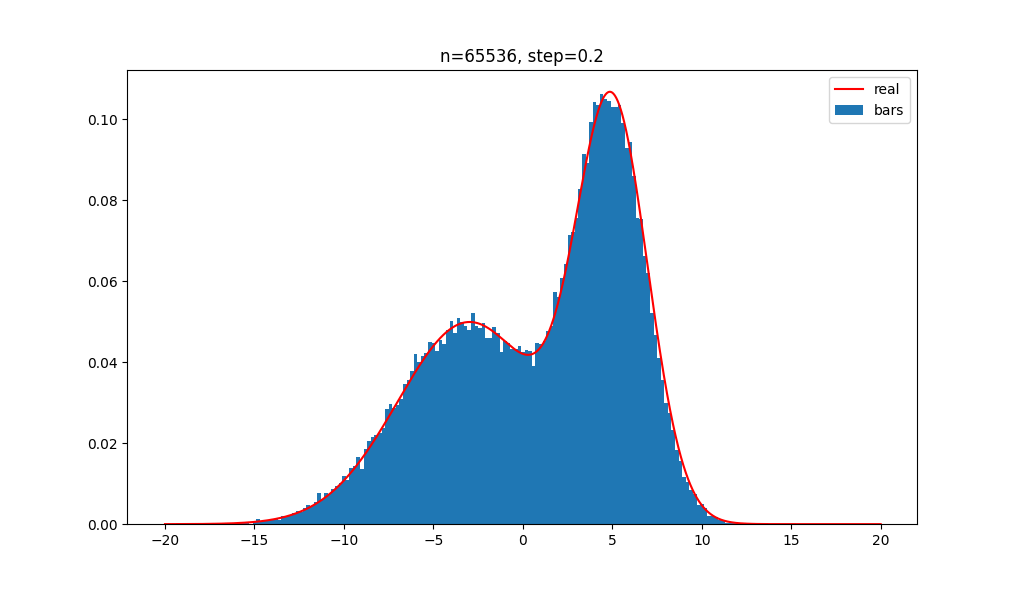
高斯窗
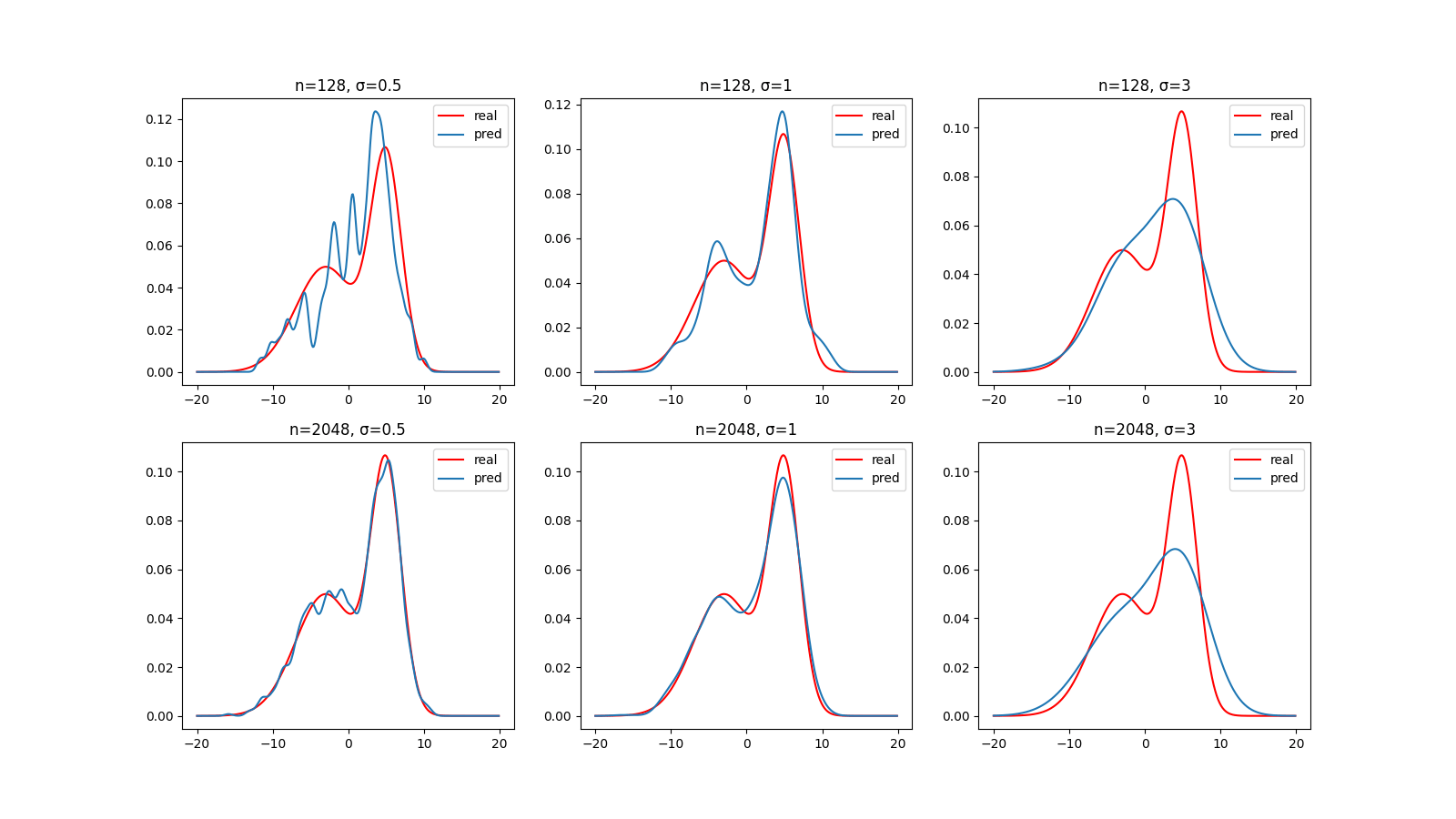
你可能发现当平滑参数过大时,估计的效果并不理想。然而在窗函数及其参数满足一定的条件时,Parzen窗估计可以是渐进无偏的。其中对于小舱体积(也就是平滑参数决定的窗口宽度)的要求是,应随着样本数的增加而趋近于0,但是缩减速度不快于。
常取为的倍数。
下面是取的高斯窗的估计结果: