本页目录

【模式识别】参数估计

上一篇提到的统计决策方法，类条件密度按已知处理。但实际问题中，往往只有已知样本，需要根据已知样本推测分布。
本章讨论的是参数估计，也就是分布的表达式形式是已知的，只是希望确定其中参数的值。

最大似然估计

假设样本的分布形式已知，现在想确定参数 $θ$ 。如果已经观测到了一些样本，记这些样本为 $χ$ ，则我们要找的参数即为：使得出现观测样本 $χ$ 概率最大的参数 $θ$ 。

考虑下面的例题：

每一个样本都形如 $X = [x_{1}, x_{2}, \dots, x_{d}]^{T}$ ，其中的每个维度都是二值变量，其分布可以由 $θ = [θ_{1}, θ_{2}, \dots, θ_{d}]^{T}$ 描述，即 $s_{i} = 1$ 的概率为 $θ_{i}$ ，相应地， $s_{i} = 0$ 的概率为 $1 - θ_{i}$ 。假设现在已经观察到样本 $χ = {X_{1}, X_{2}, \dots, X_{n}}$ ，希望估计参数 $θ$ 。

注意，如果样本有多个维度，这里记为 $X = [x_{1}, x_{2}, \dots, x_{d}]^{T}$ ， $x_{1}$ 、 $x_{2}$ 表示样本的分量；
有时，若样本只有一个维度，则样本会直接简记为 $x$ ；此时 $x_{1}$ 、 $x_{2}$ 表示两个样本。
请注意语义。

观测到样本 $χ$ 的概率为：

P (X_{1}, X_{2}, \dots, X_{n} ∣ θ) = \prod_{k = 1}^{n} P (X_{i}) = \prod_{k = 1}^{n} \prod_{i = 1}^{d} θ_{i}^{x_{ki}} (1 - θ_{i})^{1 - x_{ki}}

式子中的 $x_{ki}$ 代表第 $k$ 个样本的第 $i$ 个分量，其值为0或1。

取对数似然函数：

l (θ) = ln P = \sum_{k = 1}^{n} \sum_{i = 1}^{d} [x_{ki} ln θ_{i} + (1 - x_{ki}) ln (1 - θ_{i})]

求偏导得：

\frac{\partial l ( θ )}{\partial θ _{i}} = \sum_{k = 1}^{n} [\frac{x _{ki}}{θ _{i}} - \frac{1 - x _{ki}}{1 - θ _{i}}]

$\frac{\partial l ( θ )}{\partial θ _{i}} = 0$ 得 $\sum_{k = 1}^{n} (x_{ki} - θ_{i}) = 0$ ，即 $θ_{i} = \frac{1}{n} \sum_{k = 1}^{n} x_{ki}$

把每一个分量都叠加起来，就得到最终的参数估计：

\hat{θ} = \frac{1}{n} \sum_{k = 1}^{n} X_{k}

举一个带有具体数值的例子，假如观测到了四个样本： $[1, 0, 0]$ 、 $[1, 1, 0]$ 、 $[1, 0, 0]$ 、 $[1, 1, 1]$ ，则估计参数 $\hat{θ} = [1, 0.5, 0.25]$
其含义为，对于第一个维度，四个样本均为1，因此估计 $x_{1} = 1$ 的概率为1；对于第二个样本，四个样本中有两个为1，另外两个为0，则估计 $x_{2} = 1$ 的概率为0.5，以此类推。

正态分布下的最大似然估计

单变量正态分布

\overset{μ}{^} = \frac{1}{n} \sum x_{k}

\overset{σ}{^}^{2} = \frac{1}{n} \sum (x_{k} - \overset{μ}{^})^{2}

多变量正态分布

\hat{μ} = \frac{1}{n} \sum X_{k}

\hat{Σ} = \frac{1}{n} \sum (X_{k} - \hat{μ}) (X_{k} - \hat{μ})^{T}

贝叶斯估计

贝叶斯估计与最大似然估计一个根本的区别是，最大似然估计把未知参数当作固定的量，而贝叶斯估计把未知参数本身也看作随机变量。假设未知参数是 $θ$ ，其分布空间为 $Θ$ ，定义损失函数 $λ (θ, \hat{θ})$ 表示估计误差的损失。如果已经观测到了样本集 $χ$ ，那么我们的目标是：

最小化期望风险：

\int_{Θ} λ (θ, \hat{θ}) P (θ ∣ χ) d θ

通常情况下损失函数取 $λ (θ, \hat{θ}) = (θ - \hat{θ})^{2}$ ，此时有结论：

在给定样本集下， $θ$ 的贝叶斯估计量是 $\int_{Θ} θ P (θ ∣ χ) d θ$ 。

在平方损失函数下，贝叶斯估计的步骤是：

猜测参数的先验分布 $P (θ)$

对于参数估计问题，样本的概率密度函数形式已知为 $P (X ∣ θ)$ ，形式上求出样本集分布为：

P (χ ∣ θ) = \prod_{i} P (X_{i} ∣ θ)

利用贝叶斯公式求 $θ$ 的后验概率分布：

P (θ ∣ χ) = \frac{P ( χ ∣ θ ) P ( θ )}{\int _{Θ} P ( χ ∣ θ ) P ( θ ) d θ}

$θ$ 的贝叶斯估计量是 $\int_{Θ} θ P (θ ∣ χ) d θ$

重新理解

重述上面四个步骤，以免迷失在众多符号之中。

假设我们拿到了正态分布下的样本集 $χ = {x_{1}, x_{2}, x_{3}}$ ，其中 $x_{1} = 1.3$ ， $x_{2} = 4.1$ ， $x_{3} = 3.7$ ，已知正态分布的方差 $σ = 3$ ，现在只需要估计均值 $μ$ 。

样本集中的每个样本出现的概率 $P (x_{i} ∣ μ)$ 是可以由正态分布写出的，把所有样本的出现概率相乘，就得到了当前样本集出现的概率为 $P (χ ∣ μ)$ ，这也就是上述步骤2提到的样本集分布。

$P (χ ∣ μ)$ 是一个只含 $μ$ 的表达式。我们记

f (μ) = P (χ ∣ μ) = \frac{1}{2 π \times 3} e^{- \frac{1}{2} (\frac{1.3 - μ}{3})^{2}} \cdot \frac{1}{2 π \times 3} e^{- \frac{1}{2} (\frac{4.1 - μ}{3})^{2}} \cdot \frac{1}{2 π \times 3} e^{- \frac{1}{2} (\frac{3.7 - μ}{3})^{2}}

如果采用极大似然估计，那么做到这里对 $f (μ)$ 或 $ln f (μ)$ 求导，使得导数为0的点就是估计值 $\overset{μ}{^}$ ；取 $μ = \overset{μ}{^}$ 可以使得观测到样本集的概率 $f (μ)$ 最大。

概率论的两个学派中，频率学派认为应从客观掌握的数据来计算概率；而贝叶斯学派则认为概率是有先验和后验的，我们要计算的是后验概率，这个后验概率又是以先验概率为基础的。如果采用贝叶斯估计，会假设参数 $μ$ 存在先验分布（步骤1），这里假设 $μ$ 服从均匀分布：

P (μ) = \frac{1}{5} (0 \leq μ \leq 5)

步骤3中，公式可以重写为：

P (μ ∣ χ) = \frac{f ( μ ) P ( μ )}{\int _{0}^{5} f ( μ ) P ( μ ) d μ}

首先来看分母 $\int_{0}^{5} f (μ) P (μ) d μ$ ，其含义是综合考虑所有可能的 $μ$ 取值，求出一个“平均的”样本集出现概率。这个积分式可以求出具体数值，而不是含 $μ$ 的式子。从数学的角度可以理解为，使等号左侧后验概率密度积分为1的归一化常数。

再看其他的三个量， $P (μ ∣ χ)$ 、 $f (μ) = P (χ ∣ μ)$ 、 $P (μ)$ ，这是贝叶斯学派的经典思想：用样本修正先验概率，得到后验概率。这三个式子都可以写为仅含 $μ$ 的函数。当然，因为假设的先验分布简单（均匀分布）， $P (μ)$ 为常数。
这三个式子虽然都是 $μ$ 的函数，但描述的含义有所区别。 $P (μ ∣ χ)$ 、 $P (μ)$ 描述的是 $μ$ 的分布概率，而 $f (μ)$ 描述的是样本集的出现概率。

与最大似然估计一样，贝叶斯估计也会给出参数具体的估计值。但到此步，我们只给出了 $μ$ 的后验分布。要给出估计值，首先要明确我们的目标是什么：
最大似然估计的目标是，带入估计值可以使得样本集出现概率 $f (μ)$ 最大；
而贝叶斯估计的目标是，带入估计值可以使得期望风险（定义见上文）最小。
进一步地，在损失函数为平方误差时，有结论可以给出估计值 $\overset{μ}{^}$ 的具体数值，也就是步骤4。

贝叶斯学习

现在我们逐一考虑每一个样本。没有样本的时候，要估计的参数先验分布为 $P (θ)$ 。

观测到第一个样本 $X_{1}$ 的时候，用其来修正先验分布，也就是：

P (θ ∣ X_{1}) = \frac{P ( X _{1} ∣ θ ) \cdot P ( θ )}{\int _{Θ} P ( X _{1} ∣ θ ) \cdot P ( θ ) d θ}

现在继续观测到第二个样本 $X_{2}$ ，此时根据贝叶斯学派用数据修正先验的思想，先验分布是上一轮得到的 $P (θ ∣ X_{1})$ ，修正后的后验分布为

P (θ ∣ X_{1}, X_{2}) = \frac{P ( X _{2} ∣ θ ) \cdot P ( θ ∣ X _{1} )}{\int _{Θ} P ( X _{2} ∣ θ ) \cdot P ( θ ∣ X _{1} ) d θ}

以此递推：

P (θ ∣ X_{1}, X_{2}, X_{3}) = \frac{P ( X _{3} ∣ θ ) \cdot P ( θ ∣ X _{1} , X _{2} )}{\int _{Θ} P ( X _{3} ∣ θ ) \cdot P ( θ ∣ X _{1} , X _{2} ) d θ}

P (θ ∣ X_{1}, X_{2}, \dots, X_{N}) = \frac{P ( X _{N} ∣ θ ) \cdot P ( θ ∣ X _{1} , X _{2} , \dots , X _{N - 1} )}{\int _{Θ} P ( X _{N} ∣ θ ) \cdot P ( θ ∣ X _{1} , X _{2} , \dots , X _{N - 1} ) d θ}

贝叶斯学习程序实现

假设我们有一个方差 $s = 3$ 的正态分布样本集，均值 $m$ 待估计。

import matplotlib.pyplot as plt
import numpy
import math

#生成样本集，样本集的真实均值为m=13
Xs=numpy.random.normal(13,3,100)

#计算某个样本X出现的概率
def P(X,m,s=3):
    return numpy.exp(-(X-m)**2/(2*s*s))/(s*numpy.sqrt(2*math.pi))

#假设mX的先验分布也是一个正态分布，初始的均值m0=4、方差s0=4
m0=4
s0=4

#mX的分布区间，理论上应该是(-inf,inf)，但由于两侧足够趋近于0，这里取(-40,40)
m_lim=numpy.arange(-40,40,0.01)

#无样本时m的先验分布
pm=P(m_lim,m0,s0)

#数值积分
def numint(f):
    s=0
    step=m_lim[1]-m_lim[0]
    for i in range(len(m_lim)-1):
        s+=step*f[i]
    return s

#逐个样本学习
for i,X in enumerate(Xs):
    if (i+1)%20==0 or i<5:
        plt.plot(m_lim,pm,label=f"epoch {i+1}")

    #样本出现概率，在参数m分布区间上对应的值
    pX_m=P(X,m_lim)

    #用pX_m(数据)修正pm(先验)，得到pm_X(后验)
    pm_X = pX_m*pm / numint(pX_m*pm)

    #把第i轮得到的后验分布，视作第i+1轮迭代的先验分布
    pm=pm_X

plt.legend()
plt.show()

观察迭代结果：

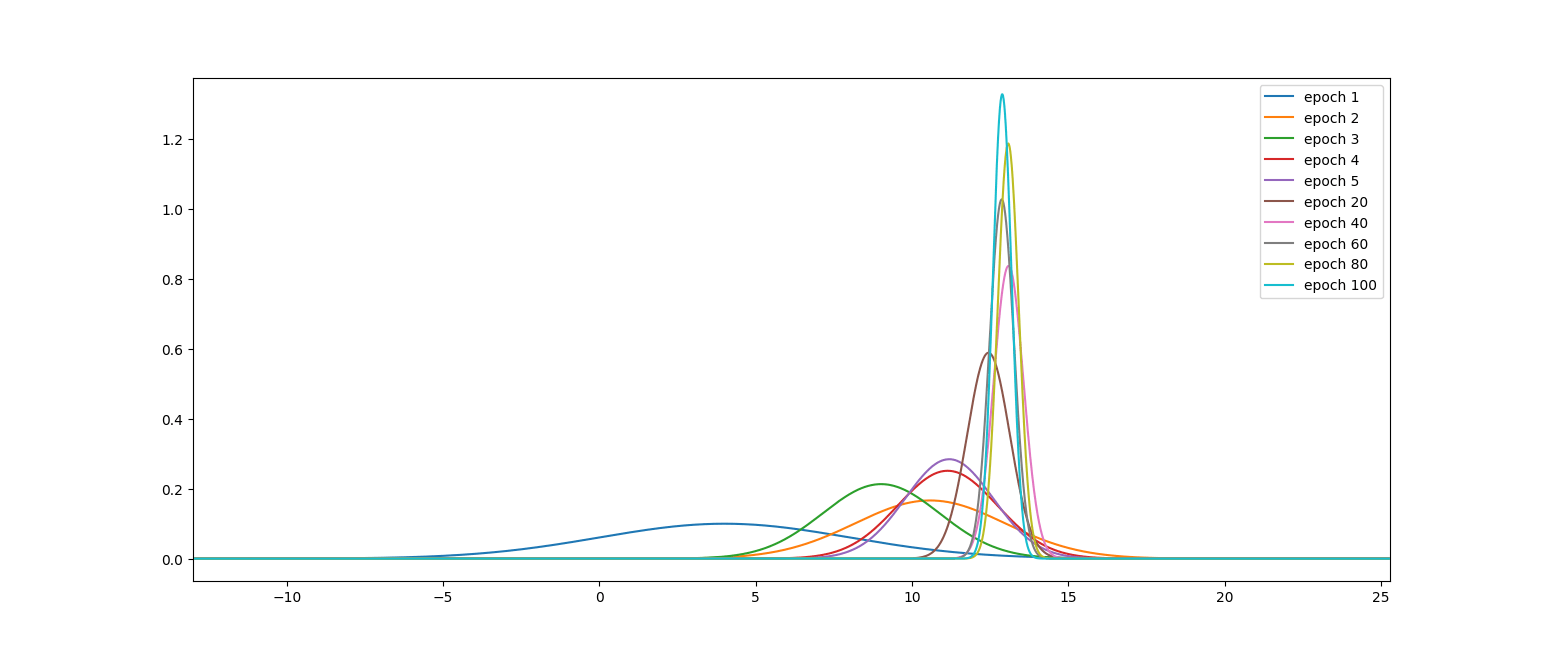
如果随着样本数增加，后验概率序列逐渐尖锐，最终趋向于以参数真实值为中心的一个尖峰，则这一过程称为贝叶斯学习。

正态分布下的贝叶斯估计

假设要估计的正态分布均值 $μ$ 未知，方差 $σ^{2}$ 已知。假定 $μ$ 的先验分布也是正态分布，均值为 $μ_{0}$ ，方差为 $σ_{0}^{2}$ 。

假设观测到的 $N$ 个样本的均值为 $m$ ，这里直接给出结论：

\overset{μ}{^} = \frac{N σ _{0}^{2}}{N σ _{0}^{2} + σ ^{2}} m + \frac{σ ^{2}}{N σ _{0}^{2} + σ ^{2}} μ_{0}

可以看到贝叶斯估计结果由两部分构成，第一项是样本知识，第二项是先验知识。

样本数量为0时，估计值完全等于先验 $μ_{0}$ ；样本数量为无穷时，估计值趋于样本均值 $m$ ；

若 $σ_{0}^{2} = 0$ ，则先验知识绝对可靠，样本不起作用；

若 $σ_{0} ≫ σ$ ，则先验知识十分不确定，估计值近似等于样本均值。

贝叶斯估计的优势在于，可以结合样本信息和先验知识，并且根据样本数量和先验知识的确定程度调和两部分信息的相对贡献。