【模式识别】统计决策方法

贝叶斯公式

考虑如下例子，记$A$为抓到方形，$B$为抓到实心图形：

$P(A)=\frac{3}{5}$，$P(B)=\frac{2}{5}$，$P(AB)=\frac{1}{5}$

抓到实心图形时抓到的是方形：$P(A|B)=\frac{1}{2}$

抓到方形时抓到的是实心图形：$P(B|A)=\frac{1}{3}$

结合上述例子理解贝叶斯公式的推导过程：

最小错误率贝叶斯决策

研究的类别有c个。

两分类情况下，最小错误率决策的四种等价规则

最小风险贝叶斯决策

条件风险

$\lambda ({\alpha }_i,{\omega }_j)$表示样本$x\in {\omega }_j$但被决策为${\omega }_i$类的损失，$i=j$表示正确决策

最小风险贝叶斯决策

研究的类别有c个，做了k个决策。

两分类情况下的最小风险贝叶斯决策

简记$\lambda ({\alpha }_i,{\omega }_j)$为${\lambda }_{ij}$：

若$R({\alpha }_1|x)<R({\alpha }_2|x)$，则$x$属于${\omega }_1$类

最小风险贝叶斯决策的另两种形式

若$({\lambda }_{21}-{\lambda }_{11})P({\omega }_1|x)>({\lambda }_{12}-{\lambda }_{22})P({\omega }_2|x)$，则决策$x\in {\omega }_1$

若$l(x)=\frac{P(x|{\omega }_1)}{P(x|{\omega }_2)}>\frac{{\lambda }_{12}-{\lambda }_{22}}{{\lambda }_{21}-{\lambda }_{11}}\cdot \frac{P({\omega }_2)}{P({\omega }_1)}$，则决策$x\in {\omega }_1$

正态分布的统计决策

从一维正态分布到高维正态分布

单变量正态分布函数：

双变量正态分布函数：

对于上述二维正态分布，记：

则用矩阵形式表示为：

理解这个长公式，先从两个概念入手：$\Sigma$矩阵代表什么？$\rho$似乎没有在通式中体现，其含义是什么？
对于二维正态分布例子中的两个变量来说，它们的协方差定义为：

$\Sigma$矩阵的含义其实是两个变量的协方差矩阵，也就是：

$\rho$的含义为两个变量的相关系数，以上述变量x1,x2为例，计算公式为：

至此就可以理解$\Sigma$,$\rho$两个参数的含义了！

正态分布概率模型下的最小错误率贝叶斯决策

注意这个类概率密度函数$P(\mathbf{X}|{\omega }_i)$的含义为，第${\omega }_i$类的样本$\mathbf{X}$的概率密度。
使用后验概率的变形作为判别函数：

从以下三种情况考虑决策面：

各类模式分布的协方差矩阵相等，样本统计独立且方差相同，协方差均为0。
此时$g(\mathbf{X})$的前两项与类别无关，后两项化简为：

如果对于上述判别函数$g(\mathbf{X})$的欧式距离项展开，并删掉与类别无关的二次项，得：

其中${\mathbf{W}}_{\mathbf{i}}=\frac{1}{{\sigma }^2}{\mathbf{\mu }}_{\mathbf{i}}$，$b=-\frac{1}{2{\sigma }^2}{{\mathbf{\mu }}_{\mathbf{i}}}^T{\mathbf{\mu }}_{\mathbf{i}}+\ln P({\omega }_i)$

判别函数是$\mathbf{X}$的线性函数，称为线性分类器。

接下来考虑决策面方程：

其中$\mathbf{W}={\mathbf{\mu }}_{\mathbf{i}}-{\mathbf{\mu }}_{\mathbf{j}}$，${\mathbf{X}}_0=\frac{1}{2}({\mathbf{\mu }}_{\mathbf{i}}+{\mathbf{\mu }}_{\mathbf{j}})-{\sigma }^2\frac{{\mathbf{\mu }}_{\mathbf{i}}-{\mathbf{\mu }}_{\mathbf{j}}}{\Vert {\mathbf{\mu }}_{\mathbf{i}}-{\mathbf{\mu }}_{\mathbf{j}}{\Vert }^2}\ln \frac{P({\omega }_i)}{P({\omega }_j)}$

这个方程确定了决策面是通过${\mathbf{X}}_0$并正交于向量$\mathbf{W}$的一个超平面。如果是二维平面上的点的分类问题，决策线过${\mathbf{X}}_0$点并且垂直于样本中心的连线。当先验概率相等时，${\mathbf{X}}_0$的后项为0，此时决策线就是样本中心连线的中垂线。
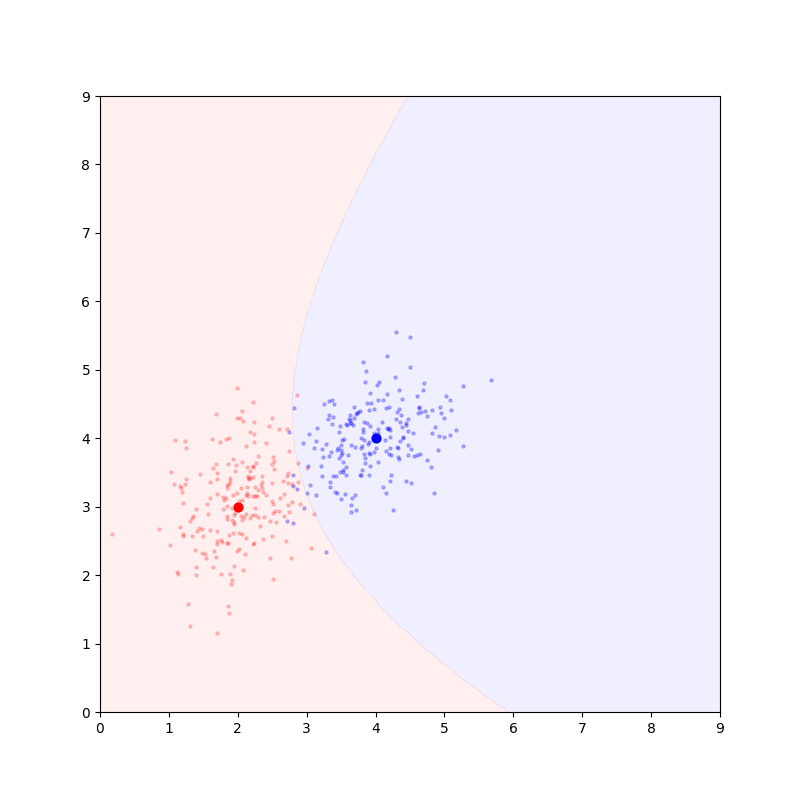
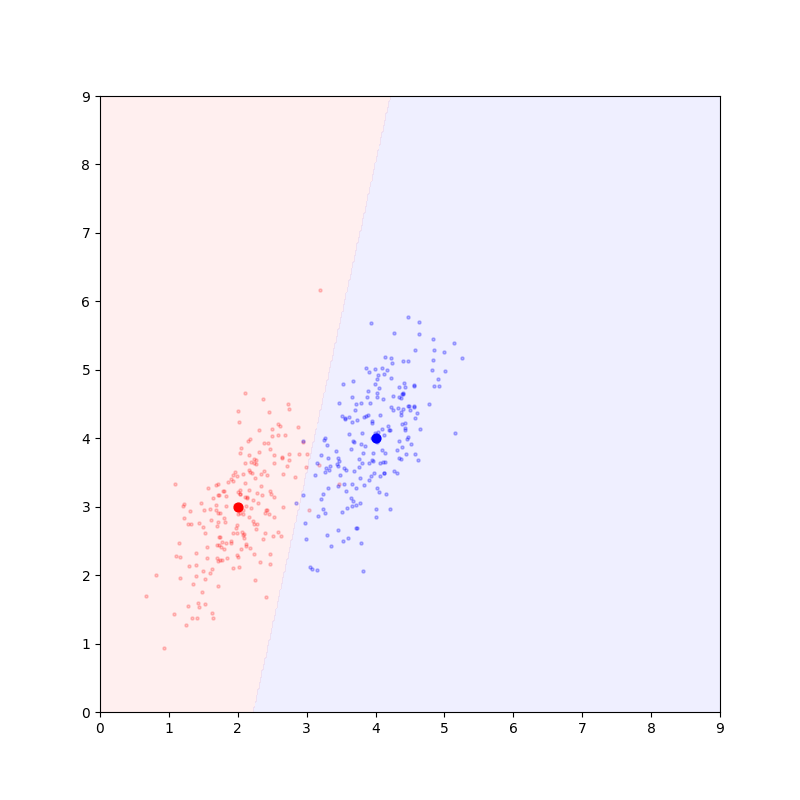
来看一个具体的例子！我们需要对平面上的点进行分类任务，第一堆样本点中心为(2,3)，第二堆样本点中心为(4,4)：

红色和蓝色分别标记了两类样本点的分布情况，其中加粗的红点和蓝点表示样本中心的位置；
生成两组样本时使用的方差均为0.8；样本的$x,y$坐标相关性为0。
现在对平面上的所有点计算判别函数g_red和g_blue。g_red更大的区域用红色阴影表示，g_blue更大的区域用蓝色阴影表示。
两个区域的交界处即为自然生成的决策线。结果如下：

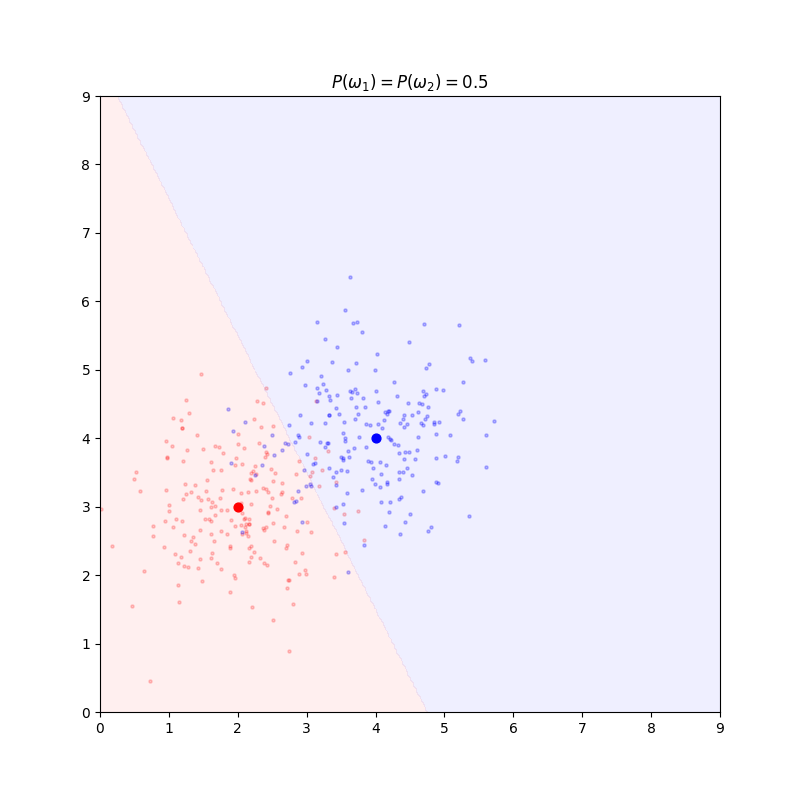
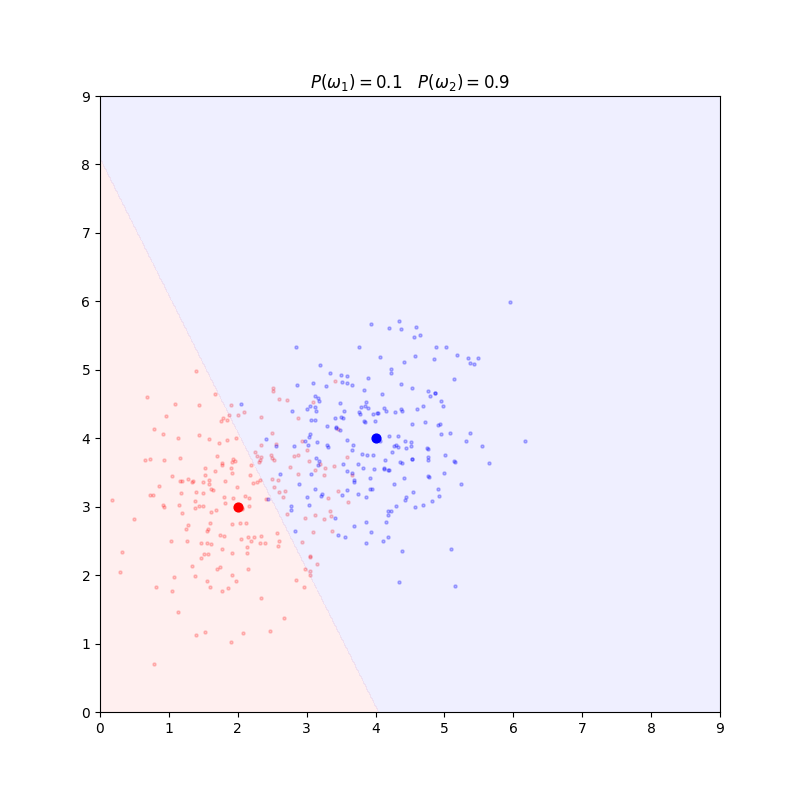
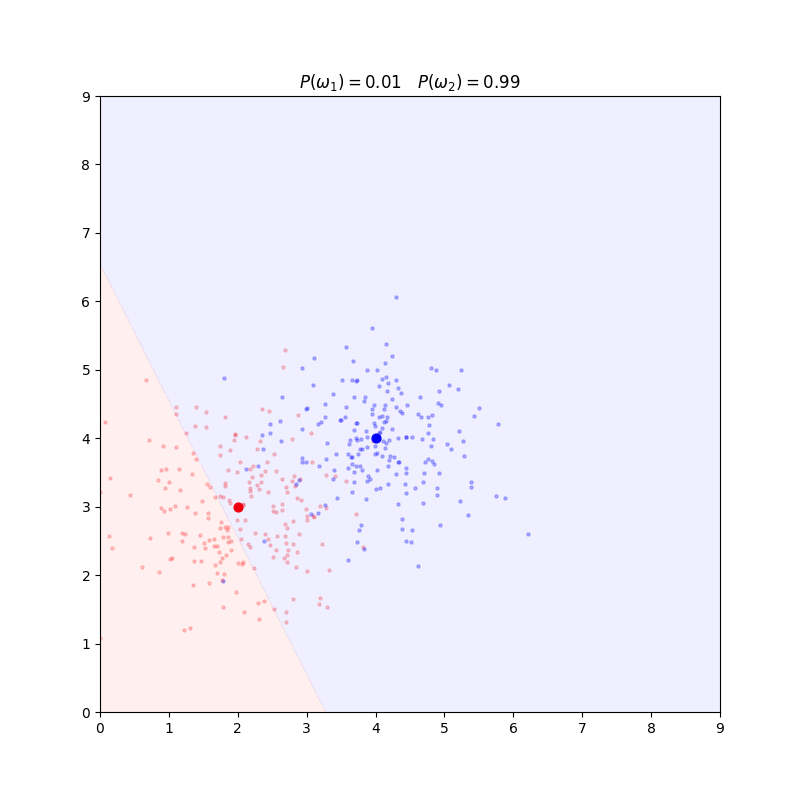
决策线垂直于样本中心的连线并且在先验概率相等的前提下过样本中心连线中点(左图)。
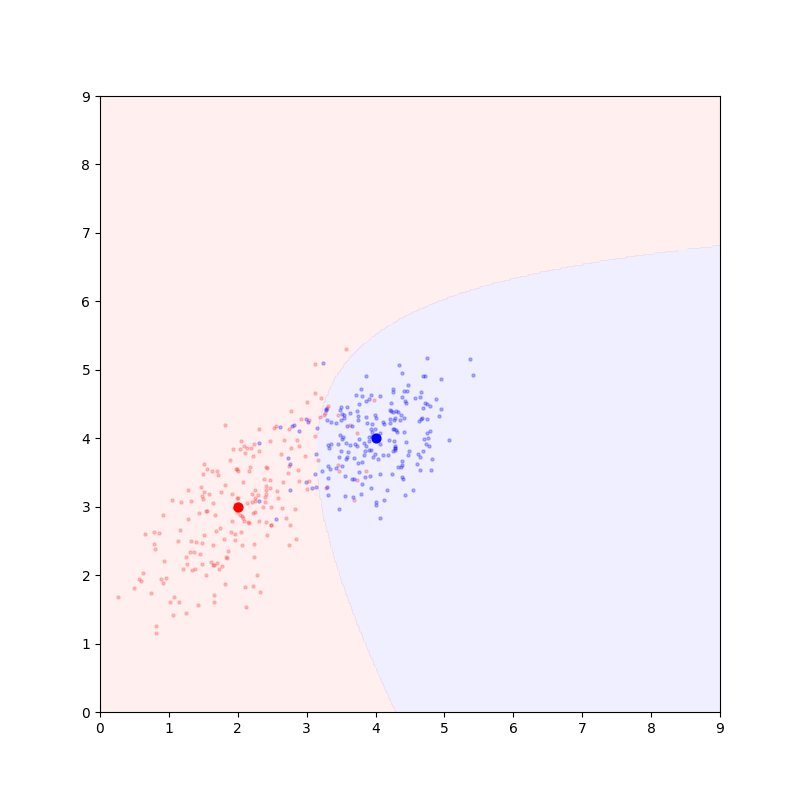
如果先验概率不相等，决策线会偏向先验概率小的一侧(中图)，而且有可能超过端点(右图)。

对于三分类问题，得到的结果类似：

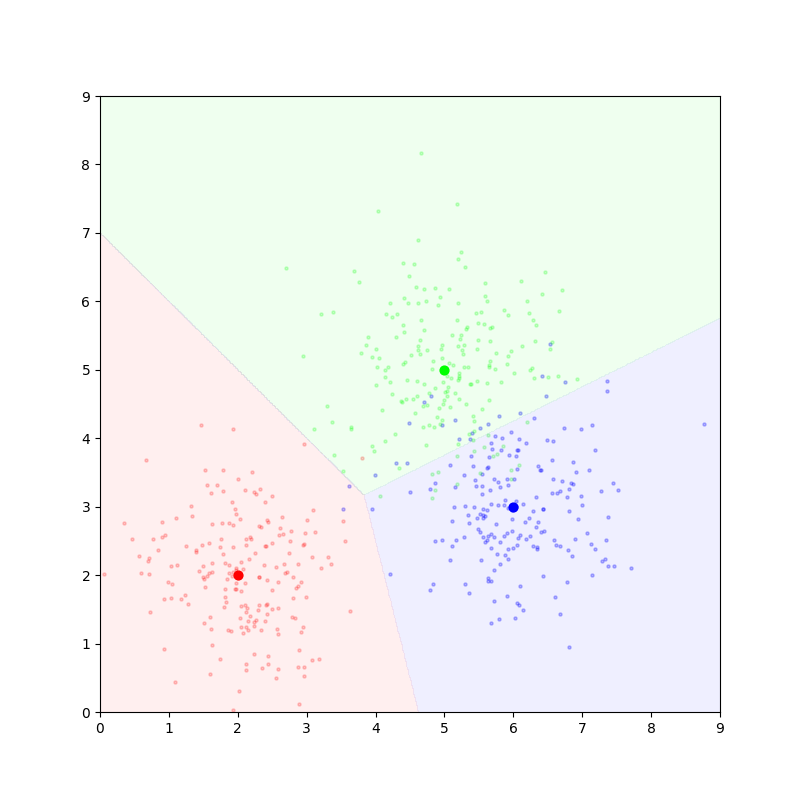
马氏距离

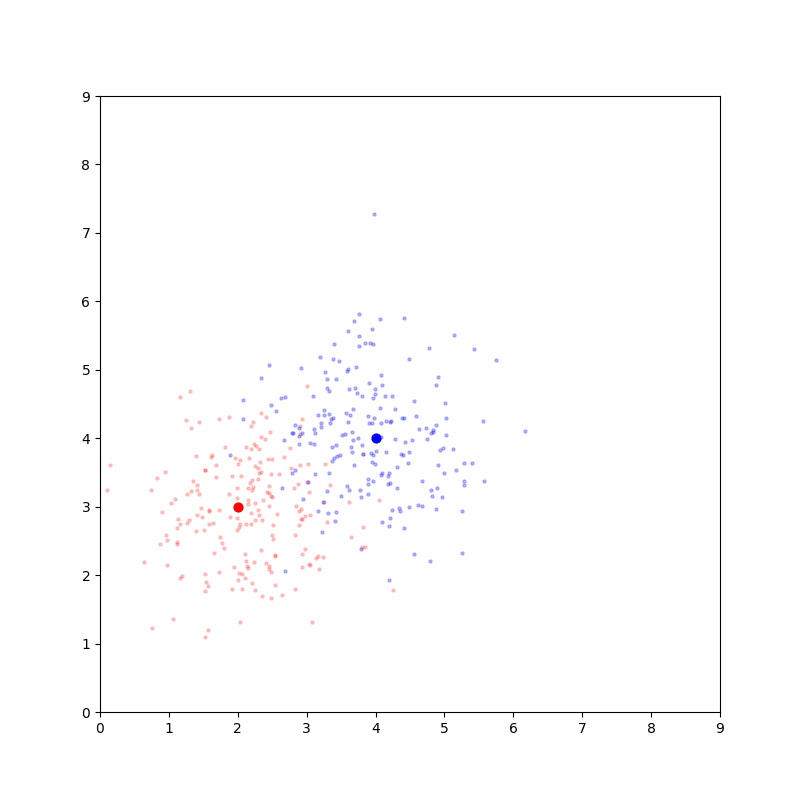
马氏距离可以看作对欧氏距离的修正。考虑下面的例子：
黑色的点距离green类样本中心更近，与red、blue类样本中心等距。它应该被归为哪一类？

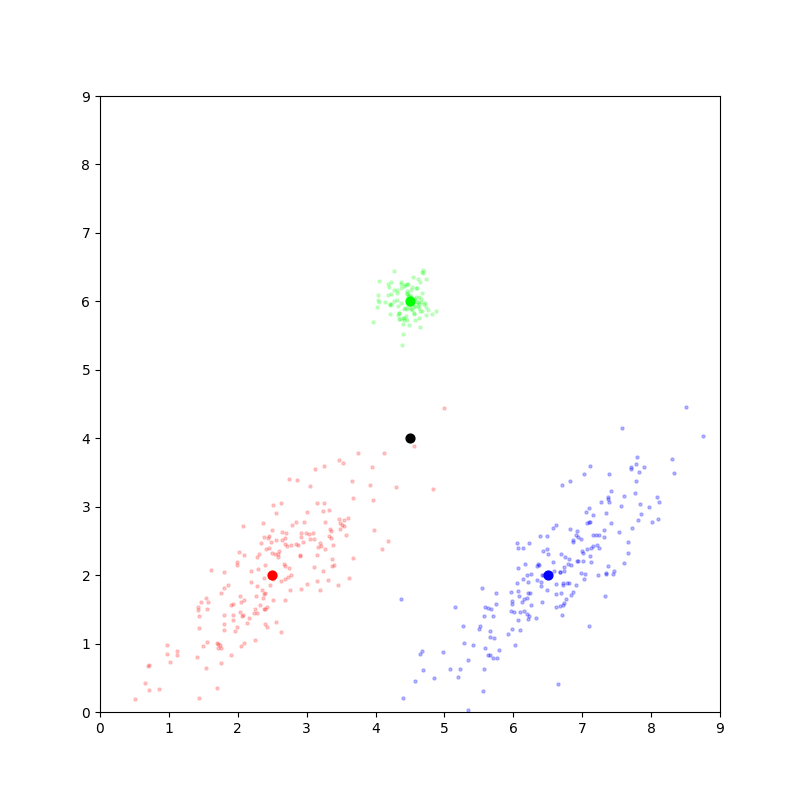
按照欧氏距离判别，它应该被归为green类；然而从直觉上判断，它更可能属于red类。
欧式距离并没有考虑样本的方差，以及样本各个维度之间的相关性。
定义马氏距离：

$r^2=(\mathbf{X}-\mathbf{\mu }{)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{X}-\mathbf{\mu })$

如果样本是二维的，且协方差矩阵$\sigma$为对角矩阵，马氏距离表示为：

$r^2=\left[\begin{array}{cc}{x}_1-{\mu }_1& x_2-{\mu }_2\end{array}\right]\left[\begin{array}{cc}1/{\sigma }_1^2& 0\\ 0& 1/{\sigma }_2^2\end{array}\right]\left[\begin{array}{c}{x}_1-{\mu }_1\\ x_2-{\mu }_2\end{array}\right]=\frac{(x_1-{\mu }_1{)}^2}{{\sigma }_1^2}+\frac{(x_2-{\mu }_2{)}^2}{{\sigma }_2^2}$

如果样本方差一样，则就是欧式距离；如果方差不一样，可以看作是标准化之后的欧氏距离。

判别函数：

决策面方程：

其中$\mathbf{W}={\mathbf{\Sigma }}^{-1}({\mathbf{\mu }}_{\mathbf{i}}-{\mathbf{\mu }}_{\mathbf{j}})$，${\mathbf{X}}_0=\frac{1}{2}({\mathbf{\mu }}_{\mathbf{i}}+{\mathbf{\mu }}_{\mathbf{j}})-\frac{{\mathbf{\mu }}_{\mathbf{i}}-{\mathbf{\mu }}_{\mathbf{j}}}{({\mathbf{\mu }}_{\mathbf{i}}-{\mathbf{\mu }}_{\mathbf{j}}{)}^T{\mathbf{\Sigma }}^{-1}({\mathbf{\mu }}_{\mathbf{i}}-{\mathbf{\mu }}_{\mathbf{j}})}\ln \frac{P({\omega }_i)}{P({\omega }_j)}$

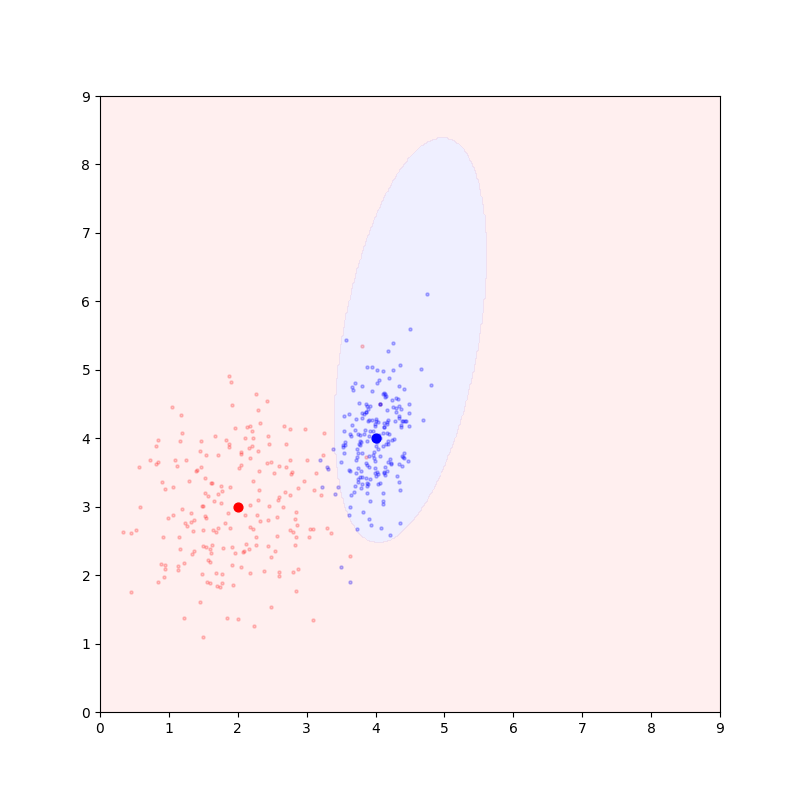
此时，先验概率相等的前提下，决策线仍然过样本中心连线中点；但不一定垂直于样本中心的连线。

此为最一般情况。决策面为超二次曲面。对于二维样本，决策线为二次曲线。
判别函数：